1.6 演習問題 〜 直線,平面
問 1.22 (
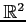 の直線)
次の
の直線)
次の
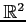 の直線に関して,
傾き,
の直線に関して,
傾き, 切片,
切片, 切片,
方向ベクトル,法線ベクトルを求めよ.
また,この直線に直交し原点を通る法線を求めよ.
切片,
方向ベクトル,法線ベクトルを求めよ.
また,この直線に直交し原点を通る法線を求めよ.
(1) 2 点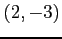 ,
,  を通る直線
(2)
を通る直線
(2)
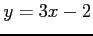 (3)
(3)
 (4)
(4)
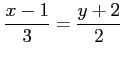
(5)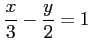
(1) 2 点
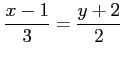
(5)
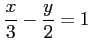
問 1.23 (
 の直線)
次の
の直線)
次の
 の直線をパラメータ表示で表せ.
また,直線の方向ベクトル,法線ベクトル,
の直線をパラメータ表示で表せ.
また,直線の方向ベクトル,法線ベクトル,
 切片,
切片, 切片,傾きを求めよ.
さらには,この直線に直交し点
切片,傾きを求めよ.
さらには,この直線に直交し点 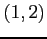 を通る法線を求めよ.
を通る法線を求めよ.
(1) 点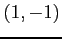 ,
, 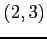 を通る直線
(2) 点
を通る直線
(2) 点 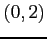 ,
,  を通る直線
を通る直線
(3) 点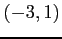 ,
, 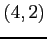 を通る直線
(4) 点
を通る直線
(4) 点 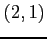 ,
, 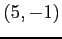 を通る直線
を通る直線
(5) (6)
(6)
 (7)
(7)
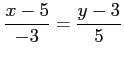
(8)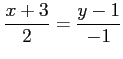 (9)
(9)  (10)
(10) 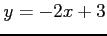 (11)
(11) 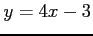 (12)
(12) 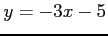
(13)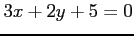 (14)
(14)  (15)
(15) 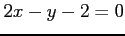 (16)
(16) 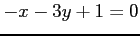
(17)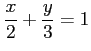 (18)
(18)
 (19)
(19)
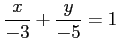 (20)
(20)
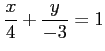
(1) 点
(3) 点
(5)
 (6)
(6)
 (7)
(7)
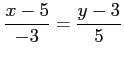
(8)
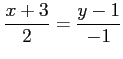 (9)
(9) (13)
(17)
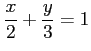 (18)
(18)
 (19)
(19)
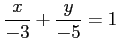 (20)
(20)
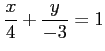
問 1.24 (
 の平面)
次の
の平面)
次の
 の平面の法線ベクトルを求めよ.
の平面の法線ベクトルを求めよ.
(1)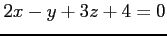 (2) 3 点
(2) 3 点 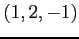 ,
, 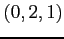 ,
, 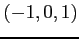 を通る平面
を通る平面
(1)
問 1.25 (
 の平面)
次の 3 点を通る
の平面)
次の 3 点を通る
 の平面の方程式を求めよ.
の平面の方程式を求めよ.
(1) 点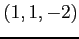 ,
,  ,
, 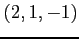 (2) 点
(2) 点  ,
, 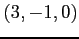 ,
, 
(3) 点 ,
, 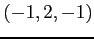 ,
, 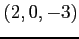 (4) 点
(4) 点 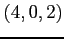 ,
, 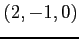 ,
, 
(1) 点
(3) 点
問 1.26 (
 の直線)
次の
の直線)
次の
 の直線の方向ベクトルを求めよ.
の直線の方向ベクトルを求めよ.
(1) 2 点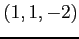 ,
,  を通る直線
を通る直線
(2) ,
, 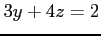 (3)
(3) 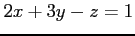 ,
, 
(1) 2 点
(2)
問 1.27 (
 の直線)
次の 2 点を通る
の直線)
次の 2 点を通る
 の直線を
パラメータ表示と成分表示で表せ.
の直線を
パラメータ表示と成分表示で表せ.
(1) 点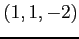 ,
,  (2) 点
(2) 点 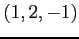 ,
, 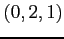 (3) 点
(3) 点  ,
, 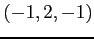
(4) 点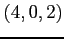 ,
, 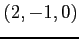 (5) 点
(5) 点  ,
, 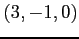
(1) 点
(4) 点
問 1.28 (
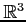 の直線)
次の
の直線)
次の
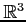 の直線をパラメータ表示せよ.
の直線をパラメータ表示せよ.
(1) ,
,
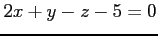 (2)
(2)
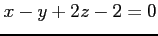 ,
,
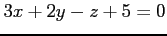
(1)
問 1.29 (平面と直交する直線)
次の
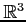 の平面と直交し点
の平面と直交し点 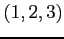 を通る直線の方程式を求めよ.
また,その交点を求めよ.
を通る直線の方程式を求めよ.
また,その交点を求めよ.
(1) (2)
(2) 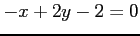 (3)
(3) 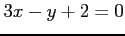 (4)
(4)

(1)
問 1.30 (直交する直線)
次の
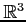 の直線と直交し点
の直線と直交し点 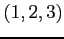 を通る直線の方程式を求めよ.
また,その交点を求めよ.
を通る直線の方程式を求めよ.
また,その交点を求めよ.
(1)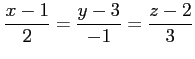 (2)
(2)
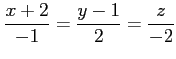
(1)
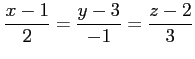 (2)
(2)
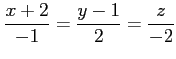
問 1.31 (平行四辺形の面積)
次の4 点からなる平行四辺形の面積を求めよ.
(1)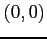 ,
, 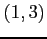 ,
,  ,
, 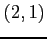 (2)
(2) 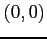 ,
, 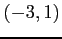 ,
,  ,
, 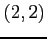
(3)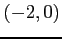 ,
, 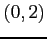 ,
, 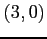 ,
, 
(1)
(3)
平成21年12月2日