1.5
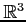 の直交する直線
の直交する直線
例 1.18 (直交する直線)
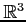 の直線
の直線
 と直交し点
と直交し点  を通る直線の方程式を求める.
求めたい直線を
を通る直線の方程式を求める.
求めたい直線を 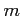 とする.
とする.
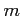 の方向ベクトルを
の方向ベクトルを
 とする.
これは直線
とする.
これは直線  の方向ベクトル
の方向ベクトル
 と直交するので,
と直交するので,
 より,
より,
が成り立つ.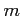 は点
は点  を通り方向ベクトル
を通り方向ベクトル  であるから,
であるから,
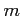 をパラメータ表示すると
をパラメータ表示すると
となる. をパラメータ表示すると
をパラメータ表示すると
となる.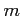 と
と  の交点
の交点 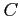 を求める.
(○),(●)より,
連立方程式
を求める.
(○),(●)より,
連立方程式
を得る. 拡大係数行列を簡約化すると,
となる. 連立方程式が一意な解をもつためには, 第 2 式の第 成分が 0 であれば良いので,
成分が 0 であれば良いので,
を得る. (☆),(★) より,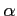 ,
, 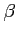 ,
, 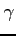 の連立方程式をつくり
それを簡約化すると,
の連立方程式をつくり
それを簡約化すると,
を得る.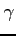 は任意であるから適当に
は任意であるから適当に  とすると,
とすると,
 ,
,  である.
よって,
である.
よって,
 ,
,
 である.
交点
である.
交点 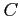 の座標は
の座標は
 と求まる.
また,
と求まる.
また,
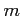 の方向ベクトルは
の方向ベクトルは
 と求まる.
よって,
と求まる.
よって,
 と得られる.
と得られる.
 と直交し点
と直交し点  とする.
これは直線
とする.
これは直線  と直交するので,
と直交するので,
が成り立つ.
となる.
となる.
 |
を得る. 拡大係数行列を簡約化すると,
 |
となる. 連立方程式が一意な解をもつためには, 第 2 式の第
を得る. (☆),(★) より,
を得る.
 ,
,
 である.
交点
である.
交点  と求まる.
また,
と求まる.
また,
 と求まる.
よって,
と求まる.
よって,
 と得られる.
と得られる.
例 1.19 (直交する直線)
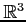 の直線
の直線
 と直交し点
と直交し点  を通る直線の方程式を求める.
求めたい直線を
を通る直線の方程式を求める.
求めたい直線を 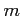 とする.
点
とする.
点 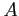 から直線
から直線  への正射影を
への正射影を 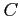 とする.
とする.
 上の適当な点
上の適当な点  をとると,
をとると,
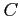 は
は
により求まる.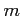 は直線
は直線  より求まる.
より求まる.
 と直交し点
と直交し点  |
により求まる.
例 1.20 (直交する直線)
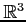 の直線
の直線
 と直交し点
と直交し点  を通る直線の方程式を求める.
求めたい直線を
を通る直線の方程式を求める.
求めたい直線を 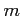 とする.
点
とする.
点 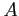 から直線
から直線  への正射影を
への正射影を 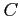 とする.
直線
とする.
直線  上の動点
上の動点 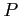 の座標は
の座標は
である.線分 の長さが最短になるとき,
の長さが最短になるとき,
 である.
である.
より, のとき最小になる.
のとき最小になる.
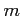 は直線
は直線  より求まる.
より求まる.
 と直交し点
と直交し点 である.線分
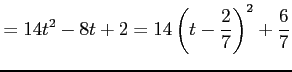 |
より,
 のとき最小になる.
のとき最小になる.
例 1.21 (直交する直線)
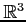 の直線
の直線
 と直交し点
と直交し点  を通る直線の方程式を求める.
求めたい直線を
を通る直線の方程式を求める.
求めたい直線を 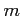 とする.
点
とする.
点 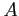 から直線
から直線  への正射影を
への正射影を 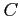 とする.
直線
とする.
直線  と直交し点
と直交し点 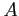 を通る平面
を通る平面 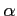 を考える.
を考える.
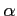 と
と  の交点が
の交点が 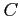 となる.
となる.
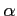 の法線ベクトルは
の法線ベクトルは  の方向ベクトルであり,
の方向ベクトルであり,
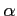 は点
は点 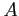 を通るので,
を通るので,
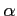 の方程式は
の方程式は
である. 直線 のパラメータ表示は
のパラメータ表示は
である.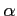 と
と  の交点を求める.
(●)を(○)へ代入すると
の交点を求める.
(●)を(○)へ代入すると
 を得る.
を得る.
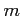 は直線
は直線  より求まる.
より求まる.
 と直交し点
と直交し点 である. 直線
である.
 を得る.
を得る.
平成21年12月2日