3.21 線積分と多重積分
定理 3.97 (グリーンの定理)
領域 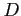 内で関数
内で関数
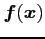 が連続なとき,
が連続なとき,
が成り立つ.
であるとき,
より,
が成り立つ. 任意に与えられた領域を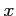 に関して単純な領域として分割し,
積分を求める.このとき重なり合う境界は向きが異なるので,
積分値は符号が反転し相殺しあう.
よって,任意の領域に対しても上式が成立する.
同様にして
に関して単純な領域として分割し,
積分を求める.このとき重なり合う境界は向きが異なるので,
積分値は符号が反転し相殺しあう.
よって,任意の領域に対しても上式が成立する.
同様にして 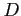 が
が 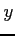 に関して単純な領域であるとすると
に関して単純な領域であるとすると
が成り立つ.これらを合わせてグリーンの定理を得る.
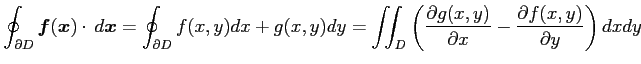 |
が成り立つ.
(証明)
![]() が
が ![]() に関して単純な領域
に関して単純な領域
であるとき,
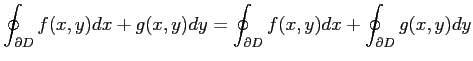 |
より,
 |
||
 |
||
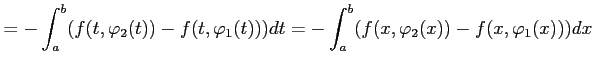 |
||
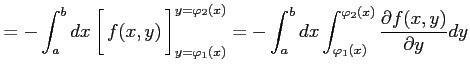 |
||
 |
が成り立つ. 任意に与えられた領域を
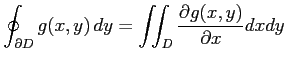 |
が成り立つ.これらを合わせてグリーンの定理を得る.
注意 3.98 (グリーンの定理)
グリーンの定理は線積分と多重積分の移り合いを表す.
例 3.99 (グリーンの定理の使用例)
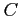 を半径
を半径 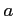 の円上を 1 周する有向曲線
の円上を 1 周する有向曲線
とする. このとき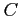 の内部の領域は
の内部の領域は
である. 領域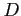 において関数
において関数 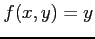 ,
, 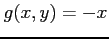 は連続であるから,
線積分
は連続であるから,
線積分
はグリーンの定理が適用でき,
と計算される.
とする. このとき
である. 領域
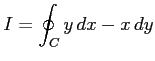 |
はグリーンの定理が適用でき,
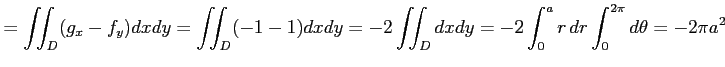 |
と計算される.
例 3.100 (グリーンの定理)
線積分
を計算する. ただし, 積分路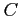 は
は 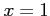 ,
, 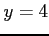 ,
, 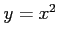 (
(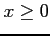 ) で囲まれる領域の境界を
正の向きに回るとする.
積分路
) で囲まれる領域の境界を
正の向きに回るとする.
積分路 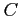 内の領域を
内の領域を
とおく. 領域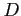 内で
内で
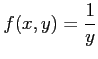 ,
,
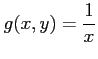 は連続であるから,
グリーンの定理が適用可能である.
これを用いると,
は連続であるから,
グリーンの定理が適用可能である.
これを用いると,
と求まる.
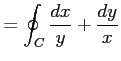 |
を計算する. ただし, 積分路
とおく. 領域
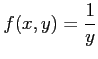 ,
,
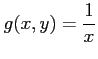 は連続であるから,
グリーンの定理が適用可能である.
これを用いると,
は連続であるから,
グリーンの定理が適用可能である.
これを用いると,
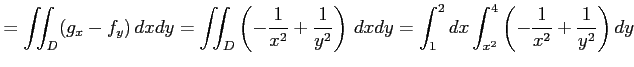 |
||
![$\displaystyle = \int_{1}^{2}dx \left[\vrule height1.5em width0em depth0.1em\,{-...
...th0em depth0.1em\,{\frac{3}{x}+\frac{3}{4}x}\,\right]_{x=1}^{x=2}= -\frac{3}{4}$](img2535.png) |
と求まる.
例 3.101 (グリーンの定理)
周回積分
を求める. ただし,積分路は ,
,
 : 中心は原点,半径
: 中心は原点,半径 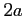 の円を正の向きに一周,
の円を正の向きに一周,
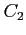 : 中心は原点,半径
: 中心は原点,半径 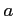 の円を負の向きに一周とする.
の円を負の向きに一周とする.
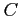 の内部の領域は
の内部の領域は
である. 領域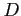 内で関数
内で関数 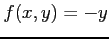 ,
, 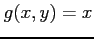 は連続であるから,
グリーンの定理が適用可能である.
線積分は
は連続であるから,
グリーンの定理が適用可能である.
線積分は
と多重積分に変わる. 極座標に置換積分すると,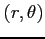 座標では
座標では
であるから,
となる.
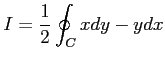 |
を求める. ただし,積分路は
である. 領域
 |
と多重積分に変わる. 極座標に置換積分すると,
であるから,
![$\displaystyle =\iint_{E}r\,drd\theta= \int_{a}^{2a}r\,dt\int_{0}^{2\pi}d\theta=...
...[\vrule height1.5em width0em depth0.1em\,{\theta}\,\right]_{0}^{2\pi}= 3\pi a^2$](img2541.png) |
となる.
例 3.102 (グリーンの定理が使用不可な例)
線積分
を考える.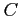 は単位円上を 1 周する有向曲線であり,
は単位円上を 1 周する有向曲線であり,
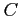 の内部の領域は
の内部の領域は
である. 関数
は原点で連続ではないので, 領域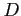 のすべての点において
関数
のすべての点において
関数 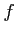 ,
, 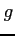 は連続ではないからグリーンの定理は適用できない.
は連続ではないからグリーンの定理は適用できない.
より,
となる. 正しくは,
と得られる.
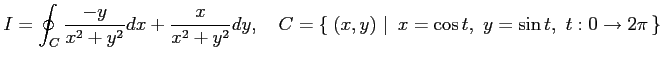 |
を考える.
である. 関数
 |
は原点で連続ではないので, 領域
誤りではあるが, グリーンの定理を適用して計算すると,
 |
より,
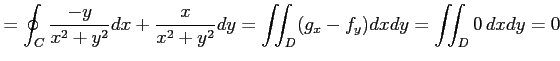 |
となる. 正しくは,
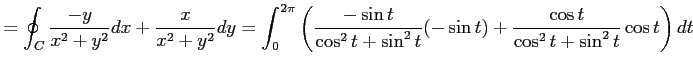 |
||
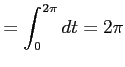 |
と得られる.
平成21年12月2日