3.24 演習問題 〜 線積分
問 3.109 (線積分)
積分路 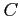 を図示しパラメータ表示し,線積分
を図示しパラメータ表示し,線積分 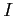 を求めよ.
を求めよ.
(1) ,
,
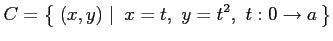
(2) ,
,
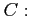 曲線
曲線 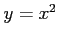 上で点
上で点 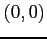 から
から  へ移動.
へ移動.
(3)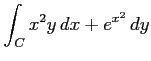 ,
,
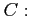 曲線
曲線 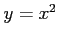 上で点
上で点  から
から 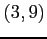 へ移動.
へ移動.
(4) ,
,
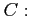 点
点  から
から 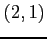 へ直線的に移動.
へ直線的に移動.
(5) ,
,
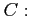 点
点  から
から 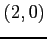 へ直線的に移動,
さらに
へ直線的に移動,
さらに 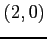 から
から 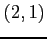 へ直線的に移動.
へ直線的に移動.
(6)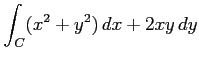 ,
,
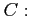 点
点 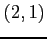 から 点
から 点 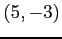 へ直線的に移動.
へ直線的に移動.
(7)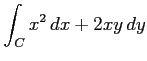 ,
,
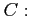
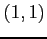 から 点
から 点  へ直線的に移動.
へ直線的に移動.
(8)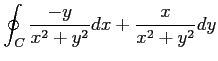 ,
,
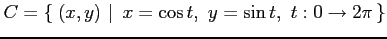
(9)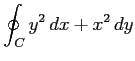 ,
,
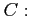
 上を正方向に一周.
上を正方向に一周.
(10)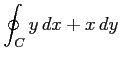 ,
,
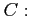
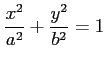 上を
正方向に一周.
上を
正方向に一周.
(11)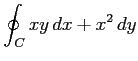 ,
,
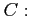 単位円を点
単位円を点  から点
から点 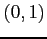 へ正方向に移動.
へ正方向に移動.
(12) ,
,
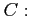
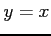 と
と 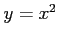 で囲まれる領域の境界を正の向きに一周.
で囲まれる領域の境界を正の向きに一周.
(13)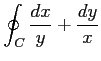 ,
,
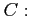
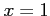 ,
, 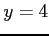 ,
, 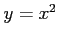 (
(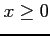 ) で囲まれる領域の境界を正の向きに回る
曲線.
) で囲まれる領域の境界を正の向きに回る
曲線.
(14)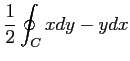 ,
,
 ,
,
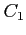 : 中心は原点,半径
: 中心は原点,半径 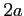 の円を正の向きに一周,
の円を正の向きに一周,
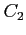 : 中心は原点,半径
: 中心は原点,半径 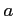 の円を負の向きに一周.
の円を負の向きに一周.
(1)
 ,
,
(2)
 ,
,
(3)
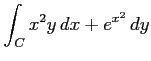 ,
,
(4)
 ,
,
(5)
 ,
,
(6)
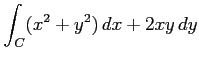 ,
,
(7)
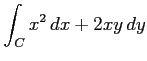 ,
,
(8)
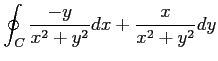 ,
,
(9)
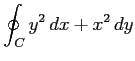 ,
,
(10)
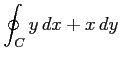 ,
,
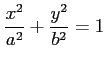 上を
正方向に一周.
上を
正方向に一周.
(11)
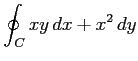 ,
,
(12)
 ,
,
(13)
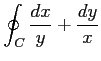 ,
,
(14)
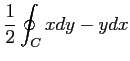 ,
,
問 3.110 (グリーンの定理)
次の線積分をグリーンの定理を用いて計算せよ.
(1)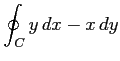 ,
,
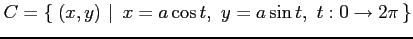
(2)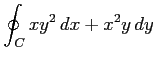 ,
,
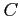 : 単位円上を正方向に一周.
: 単位円上を正方向に一周.
(3)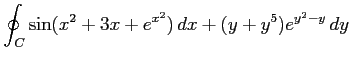 ,
,
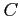 : 単位円上を正方向に一周.
: 単位円上を正方向に一周.
(4)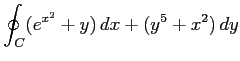 ,
,
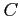 : 単位円上を正方向に一周.
: 単位円上を正方向に一周.
(5)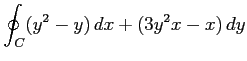 ,
,
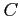 : 単位円上を正方向に一周.
: 単位円上を正方向に一周.
(6)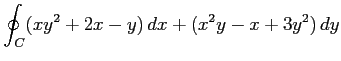 ,
,
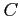 : 単位円上を正方向に一周.
: 単位円上を正方向に一周.
(7)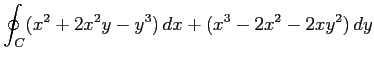 ,
,
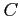 : 単位円上を正方向に一周.
: 単位円上を正方向に一周.
(8)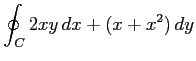 ,
,
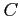 : 単位円上を正方向に一周.
: 単位円上を正方向に一周.
(9)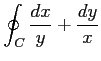 ,
,
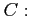
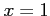 ,
, 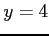 ,
, 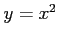 (
(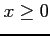 ) で囲まれる領域の境界を正の向きに回る
曲線.
) で囲まれる領域の境界を正の向きに回る
曲線.
(10)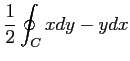 ,
,
 ,
,
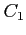 : 中心は原点,半径
: 中心は原点,半径 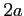 の円を正の向きに一周,
の円を正の向きに一周,
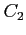 : 中心は原点,半径
: 中心は原点,半径 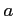 の円を負の向きに一周.
の円を負の向きに一周.
(1)
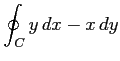 ,
,
(2)
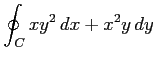 ,
,
(3)
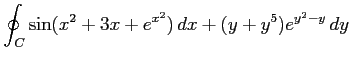 ,
,
(4)
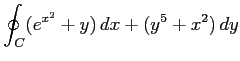 ,
,
(5)
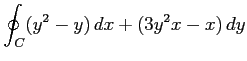 ,
,
(6)
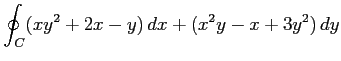 ,
,
(7)
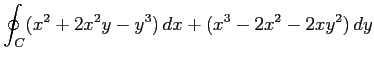 ,
,
(8)
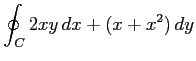 ,
,
(9)
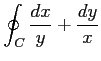 ,
,
(10)
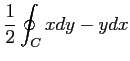 ,
,
問 3.111 (線積分による面積の計算)
単一曲線内 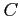 で囲まれる領域
で囲まれる領域 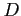 の面積
の面積 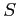 は
は
で与えられることを グリーンの定理を用いて示せ. ただし,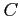 は正の向きにまわる曲線とする.
は正の向きにまわる曲線とする.
 |
で与えられることを グリーンの定理を用いて示せ. ただし,
問 3.112 (線積分による面積の計算)
次の曲線 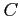 で囲まれてできる領域
で囲まれてできる領域 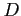 の面積
の面積 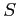 を
を
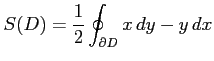 により求めよ.
により求めよ.
(1) アステロイド
(2) カーディオイド
(3)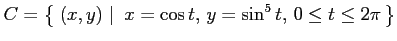
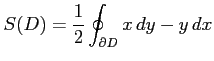 により求めよ.
により求めよ.
(1) アステロイド
(2) カーディオイド
(3)
問 3.113 (経路に依存しない線積分)
次の線積分 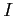 の値を求めよ.
の値を求めよ.
(1)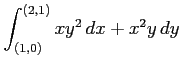
(2)
(3)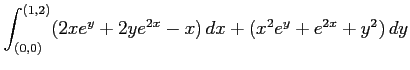
(1)
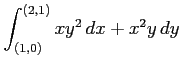
(2)

(3)
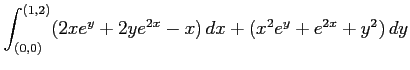
平成21年12月2日