Next: 逆三角関数の微分 Up: 微分法 Previous: 指数関数の微分 Contents
三角関数の微分
定理 3.27 (三角関数の微分)
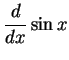 |
(325) | |
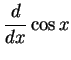 |
(326) | |
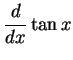 |
 |
(327) |
問 3.28
これを示せ.
を得る.ここで
であることを用いると
を得る.
を得る.ここで
であることを用いると
を得る.
であるから商の微分公式より
を得る.
(証明)
![]() とおく.定義に従い計算すると,
とおく.定義に従い計算すると,
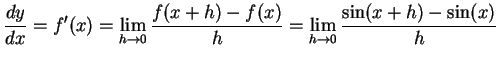 |
(328) |
を得る.ここで
 |
(329) | |
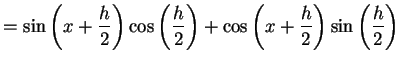 |
(330) | |
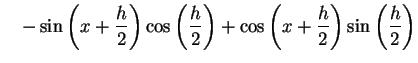 |
(331) | |
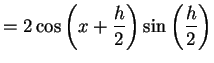 |
(332) |
であることを用いると
 |
(333) | |
 |
(334) |
を得る.
次に
![]() とおく.定義に従い計算すると,
とおく.定義に従い計算すると,
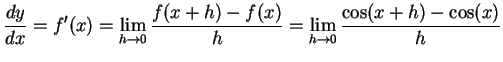 |
(335) |
を得る.ここで
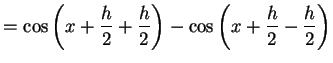 |
(336) | |
 |
(337) | |
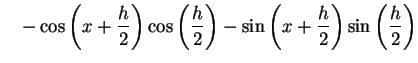 |
(338) | |
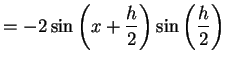 |
(339) |
であることを用いると
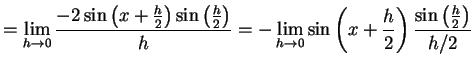 |
(340) | |
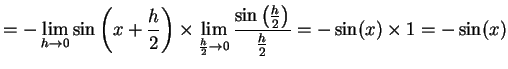 |
(341) |
を得る.
最後に
![]() を考える.このとき
を考える.このとき
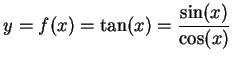 |
(342) |
であるから商の微分公式より
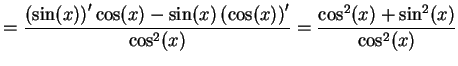 |
(343) | |
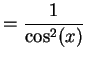 |
(344) |
を得る.
Next: 逆三角関数の微分 Up: 微分法 Previous: 指数関数の微分 Contents
Kondo Koichi
Created at 2002/09/12