Next: 双曲線関数の微分 Up: 微分法 Previous: 三角関数の微分 Contents
逆三角関数の微分
定理 3.29 (逆三角関数の微分)
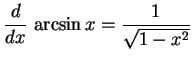 |
(345) |
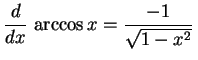 |
(346) |
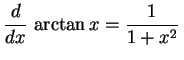 |
(347) |
問 3.30
これを示せ.
である. このとき の逆関数とその微分は
の逆関数とその微分は
である.ここで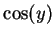 を
を  の関数で表すことを考える.
の関数で表すことを考える.
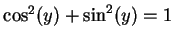 と
と 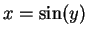 より
より
となる. 符号を片方のみ採用する.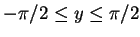 より
より
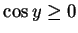 となるので,
上式の右辺も 0 以上でなければならない.
よって
となるので,
上式の右辺も 0 以上でなければならない.
よって
である.以上より
を得る.
である. 主値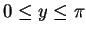 に注意して
に注意して
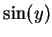 を
を  の関数で表わすと
の関数で表わすと
である.ここで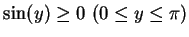 を用いた.
以上より
を用いた.
以上より
を得る.
となる.これより
を得る.
(証明)
![]() とおく.
主値を考えているので値域は
とおく.
主値を考えているので値域は
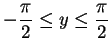 |
(348) |
である. このとき
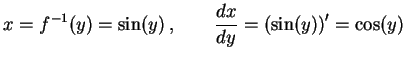 |
(349) |
である.ここで
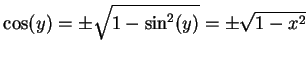 |
(350) |
となる. 符号を片方のみ採用する.
| (351) |
である.以上より
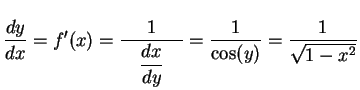 |
(352) |
を得る.
次に
![]()
![]() とおく.
この逆関数とその微分は
とおく.
この逆関数とその微分は
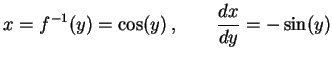 |
(353) |
である. 主値
| (354) |
である.ここで
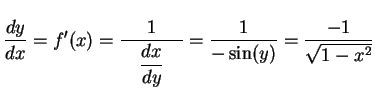 |
(355) |
を得る.
最後に
![]() を考える.
この逆関数とその微分は
を考える.
この逆関数とその微分は
| (356) | ||
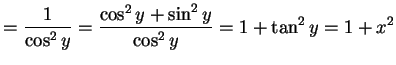 |
(357) |
となる.これより
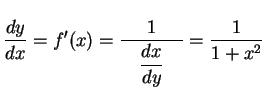 |
(358) |
を得る.
Next: 双曲線関数の微分 Up: 微分法 Previous: 三角関数の微分 Contents
Kondo Koichi
Created at 2002/09/12