Next: 逆双曲線関数の微分 Up: 微分法 Previous: 逆三角関数の微分 Contents
双曲線関数の微分
定理 3.31 (双曲線関数の微分)
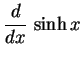 |
(359) | |
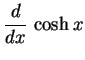 |
(360) | |
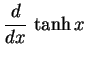 |
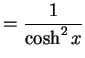 |
(361) |
問 3.32
これを示せ.
を得る.次に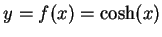 とおく.
このとき
とおく.
このとき
を得る. 最後に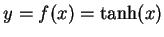 とおく.
このとき
とおく.
このとき
を得る.
![]() とおく.
このとき
とおく.
このとき
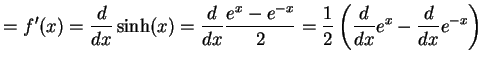 |
(362) | |
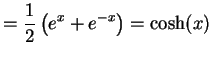 |
(363) |
を得る.次に
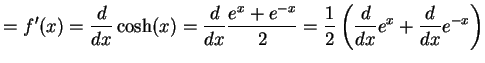 |
(364) | |
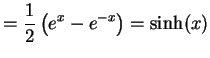 |
(365) |
を得る. 最後に
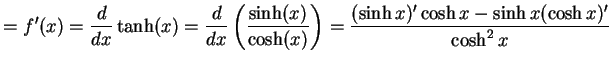 |
(366) | |
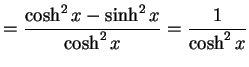 |
(367) |
を得る.
Kondo Koichi
Created at 2002/09/12