Next: テイラー展開 Up: テイラー級数 Previous: 巾級数 Contents
テイラー級数
巾級数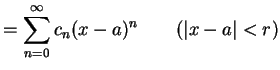 |
(427) | |
| (428) |
とおく. 数列
| 数列: |
(429) |
との対応関係がある. それでは関数
| 関数: |
(430) |
を考える.
定理 4.7 (テイラー級数)
関数  が
が  回微分可能なとき,
回微分可能なとき,
が成り立つ. ただし点 は定義内のある点とする.
この巾級数を関数
は定義内のある点とする.
この巾級数を関数  に関する
に関する  まわりの
テイラー級数(Taylor series)と呼ぶ.
特に
まわりの
テイラー級数(Taylor series)と呼ぶ.
特に 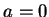 のときは,
マクローリン級数(Maclaurin series)と呼ぶ.
のときは,
マクローリン級数(Maclaurin series)と呼ぶ.
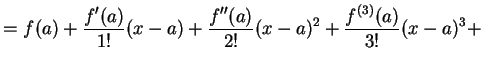 |
(431) | |
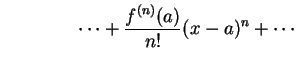 |
(432) | |
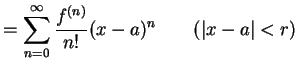 |
(433) |
が成り立つ. ただし点
注意 4.8 (テイラー級数の収束半径)
テイラー級数は巾級数
 を
を
とおいたものである. よってテイラー級数の収束半径は
により求まる.
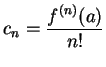 |
(434) |
とおいたものである. よってテイラー級数の収束半径は
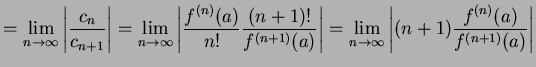 |
(435) |
により求まる.
例 4.9 (テイラー級数の具体例)
基本的な関数のテイラー級数を次に列挙する.
- (1)
-
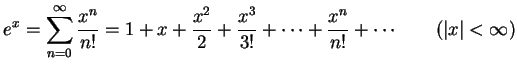
- (2)
-
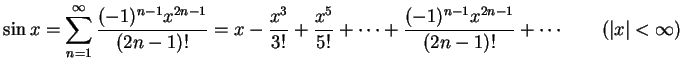
- (3)
-
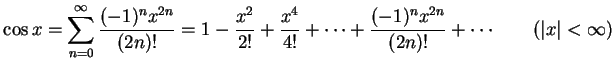
- (4)
-
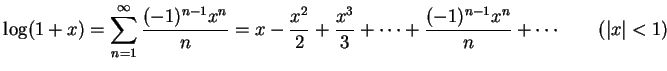
- (5)
-
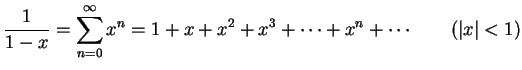
- (6)
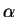 を自然数以外の実数とする.
を自然数以外の実数とする.
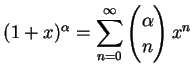
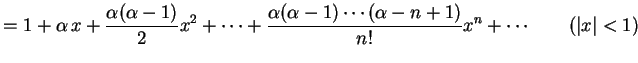
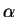 を自然数とする.
を自然数とする.
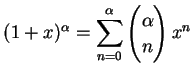
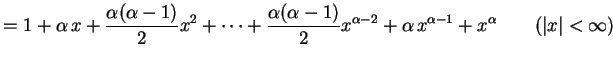
問 4.10
これを示せ.
収束半径も求めよ.
となる. 点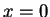 における微分係数は
における微分係数は
である. よってテーラー級数は
と求まる. 巾級数 の
収束半径
の
収束半径  を求める.
係数は
を求める.
係数は
であるから, 収束半径として
を得る.
である.一般的に書くと
である.点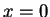 における微分係数は
における微分係数は
と求まる. これを用いてテーラー級数を求めると
を得る. 収束半径を求める.
とおくと
が得られる.
となる.一般的には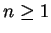 に対して
に対して
と表わされる. 点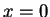 における微分係数は
における微分係数は
となる. よってテーラー級数は
と得られる. 収束半径 を求める.
を求める.
とおくと,
と得られる.
である. 一般的には
と表わされる. 点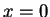 における微分係数は
における微分係数は
と得られる. よってテーラー級数は
となる. 収束半径 は
は  とおくと
とおくと
と得られる.
である.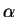 が自然数の場合と,
それ以外の場合に分けて考える.
まず
が自然数の場合と,
それ以外の場合に分けて考える.
まず 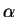 が自然数以外の実数のときを考える.
導関数は
が自然数以外の実数のときを考える.
導関数は
と表わされる. 点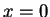 における微分係数は
における微分係数は
となる. よってテーラー級数は
と求まる. 収束半径 は
は
とおくと,
と得られる. 次に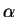 が自然数のときを考える.
導関数は
が自然数のときを考える.
導関数は
と表わされる. 点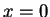 における微分係数は
における微分係数は
と求まる. よってテーラー級数は
と得られる. この展開式は有限項の和であり,有限次数の多項式である.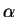 が自然数のときのテーラー展開は
二項展開となる.
展開式は多項式であり任意の実数
が自然数のときのテーラー展開は
二項展開となる.
展開式は多項式であり任意の実数  に対して成立する.
よって
に対して成立する.
よって
 であり,収束半径は
であり,収束半径は  となる.
となる.
(答え)
(1)
![]() とおく.
導関数を計算すると
とおく.
導関数を計算すると
| (436) |
となる. 点
| (437) |
である. よってテーラー級数は
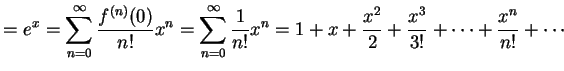 |
(438) |
と求まる. 巾級数
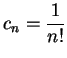 |
(439) |
であるから, 収束半径として
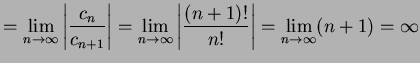 |
(440) |
を得る.
(2)
![]() とおく.
導関数を計算すると
とおく.
導関数を計算すると
| (441) |
である.一般的に書くと
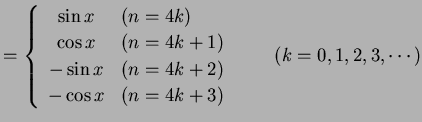 |
(442) |
である.点
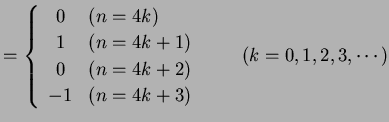 |
(443) |
と求まる. これを用いてテーラー級数を求めると
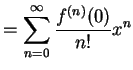 |
(444) | |
| (445) | ||
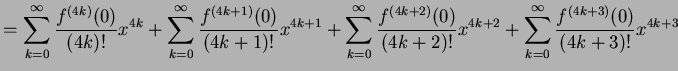 |
(446) | |
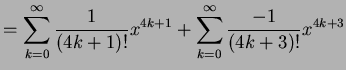 |
(447) | |
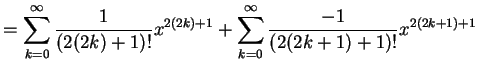 |
(448) | |
| (449) | ||
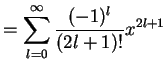 |
(450) | |
| (451) | ||
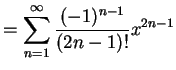 |
(452) |
を得る. 収束半径を求める.
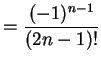 |
(453) |
とおくと
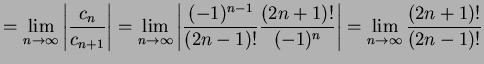 |
(454) | |
| (455) |
が得られる.
(4)
![]() とおく.
導関数を計算すると
とおく.
導関数を計算すると
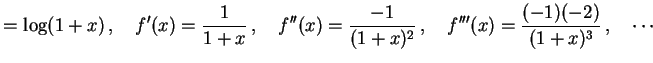 |
(456) |
となる.一般的には
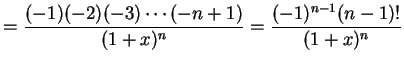 |
(457) |
と表わされる. 点
| (458) |
となる. よってテーラー級数は
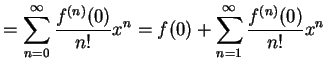 |
(459) | |
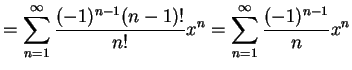 |
(460) |
と得られる. 収束半径
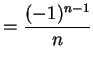 |
(461) |
とおくと,
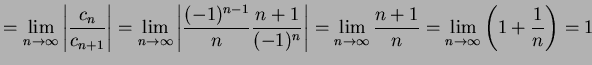 |
(462) |
と得られる.
(5)
![]() とおく.
導関数を計算すると
とおく.
導関数を計算すると
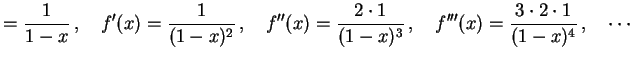 |
(463) |
である. 一般的には
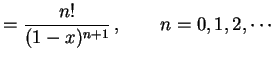 |
(464) |
と表わされる. 点
| (465) |
と得られる. よってテーラー級数は
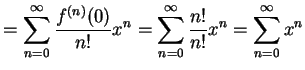 |
(466) |
となる. 収束半径
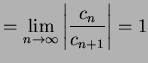 |
(467) |
と得られる.
(6)
![]() とおく.
導関数を計算すると
とおく.
導関数を計算すると
| (468) | ||
| (469) |
である.
| (470) | ||
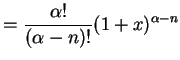 |
(471) |
と表わされる. 点
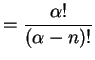 |
(472) |
となる. よってテーラー級数は
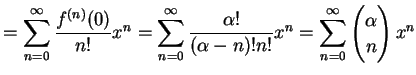 |
(473) |
と求まる. 収束半径
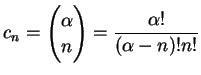 |
(474) |
とおくと,
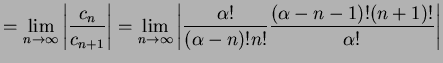 |
(475) | |
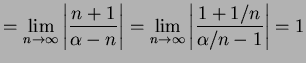 |
(476) |
と得られる. 次に
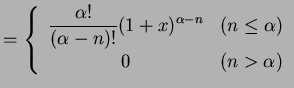 |
(477) |
と表わされる. 点
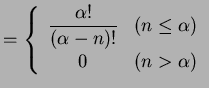 |
(478) |
と求まる. よってテーラー級数は
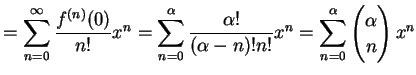 |
(479) |
と得られる. この展開式は有限項の和であり,有限次数の多項式である.
問 4.11
教科書(p.191)問題 7-5 2, 3.
定義 4.12 (階乗の拡張)
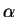 を実数とする.このとき
を実数とする.このとき 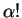 を
を
と定義する.
| (480) |
と定義する.
例 4.13 (階乗の具体例)
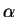 が自然数
が自然数 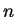 のとき
のとき
である.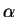 が自然数ではないとき
が自然数ではないとき
となり無限積で表わされる. 例えば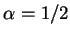 のときは
のときは
となる.
| (481) |
である.
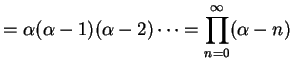 |
(482) |
となり無限積で表わされる. 例えば
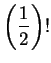 |
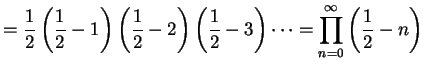 |
(483) |
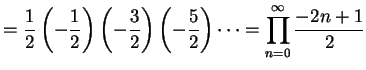 |
(484) |
となる.
定義 4.14 (二項係数の拡張)
実数 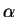 , 自然数
, 自然数 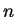 に対して
に対して
と定義する.
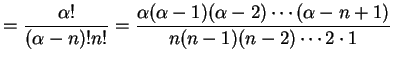 |
(485) |
と定義する.
例 4.15 (二項係数の具体例)
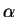 が自然数
が自然数 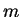 のときは
のときは
であり通常の二項係数と等しい.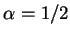 ,
, 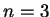 のとき
のとき
となる.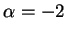 ,
, 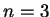 のとき
のとき
となる.
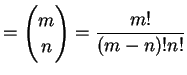 |
(486) |
であり通常の二項係数と等しい.
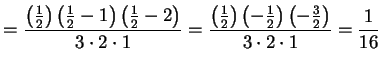 |
(487) |
となる.
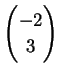 |
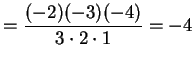 |
(488) |
となる.
注意 4.16 (三角関数と指数関数)
三角関数と指数関数は
の関係にある. ここで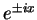 は複素指数関数である.
複素指数関数は複素数
は複素指数関数である.
複素指数関数は複素数 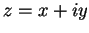 に対して
に対して
と定義される. 右辺は複素巾級数である. この定義より関係式が自然に導出される. このとき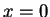 とし
とし 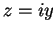 とおく.
すると
とおく.
すると
を得る. 同様に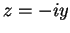 とおくと
とおくと
を得る. これより最初の関係式を得る.
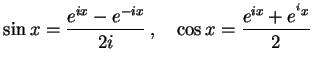 |
(489) |
の関係にある. ここで
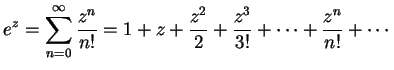 |
(490) |
と定義される. 右辺は複素巾級数である. この定義より関係式が自然に導出される. このとき
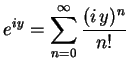 |
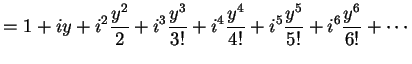 |
(491) |
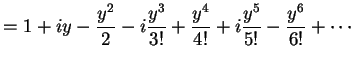 |
(492) | |
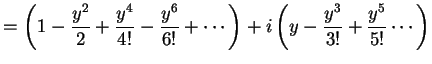 |
(493) | |
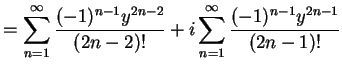 |
(494) | |
| (495) |
を得る. 同様に
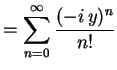 |
(496) | |
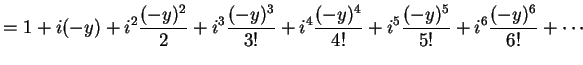 |
(497) | |
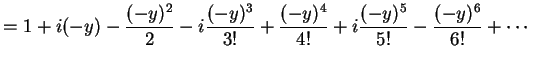 |
(498) | |
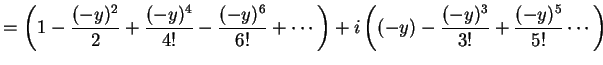 |
(499) | |
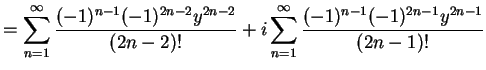 |
(500) | |
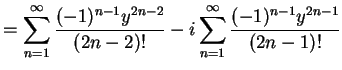 |
(501) | |
| (502) |
を得る. これより最初の関係式を得る.
Next: テイラー展開 Up: テイラー級数 Previous: 巾級数 Contents
Kondo Koichi
Created at 2002/09/12