Next: 置換積分法 Up: 積分法 Previous: 不定積分の性質 Contents
不定積分の基本的な計算
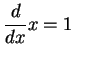 |
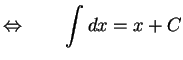 |
(680) |
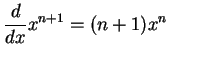 |
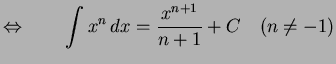 |
(681) |
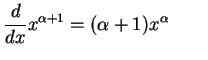 |
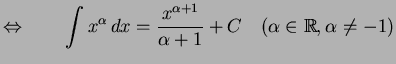 |
(682) |
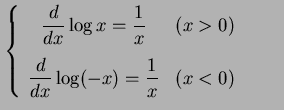 |
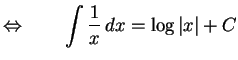 |
(683) |
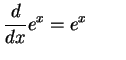 |
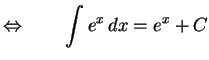 |
(684) |
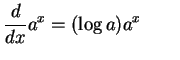 |
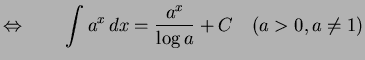 |
(685) |
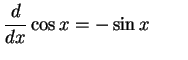 |
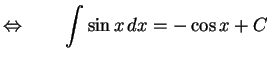 |
(686) |
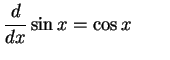 |
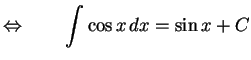 |
(687) |
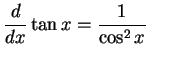 |
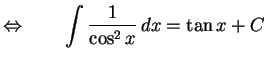 |
(688) |
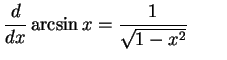 |
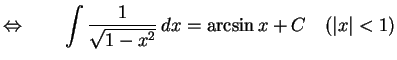 |
(689) |
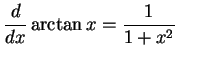 |
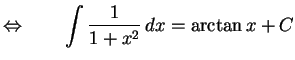 |
(690) |
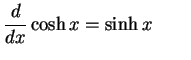 |
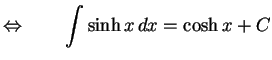 |
(691) |
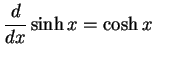 |
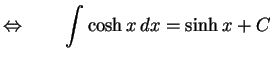 |
(692) |
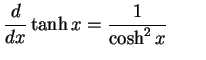 |
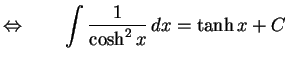 |
(693) |
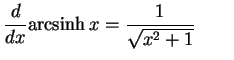 |
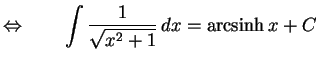 |
(694) |
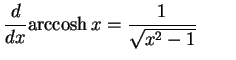 |
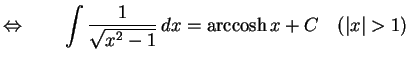 |
(695) |
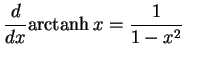 |
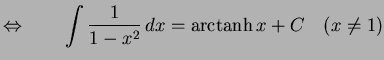 |
(696) |
例 5.4
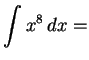 |
(697) | |
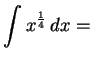 |
(698) | |
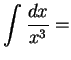 |
(699) | |
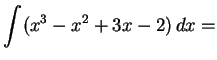 |
(700) |
Next: 置換積分法 Up: 積分法 Previous: 不定積分の性質 Contents
Kondo Koichi
Created at 2002/09/12