Next: 5 解析関数 Up: 5 テイラー級数 Previous: 3 テイラー級数の導出 Contents
4 テイラー級数の具体例
例 5.9 (指数関数のテイラー級数)
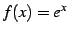 とおく.
導関数を計算すると
とおく.
導関数を計算すると
となる. 点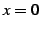 における微分係数は
における微分係数は
である. よってテーラー級数は
と求まる. 巾級数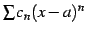 の
収束半径
の
収束半径 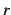 を求める.
係数は
を求める.
係数は
であるから, 収束半径として
を得る.
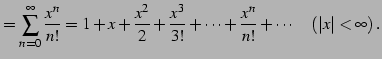 |
(559) |
(導出)
| (560) |
となる. 点
| (561) |
である. よってテーラー級数は
 |
(562) |
と求まる. 巾級数
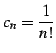 |
(563) |
であるから, 収束半径として
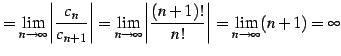 |
(564) |
を得る.
例 5.10 (三角関数のテイラー級数)
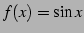 とおく.
導関数を計算すると
とおく.
導関数を計算すると
である.一般的に書くと
である.点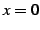 における微分係数は
における微分係数は
と求まる. これを用いてテーラー級数を求めると
を得る. 収束半径を求める.
とおくと
が得られる.
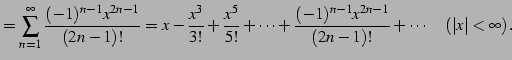 |
(565) | |
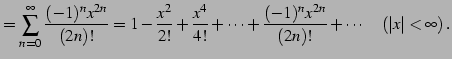 |
(566) |
(導出)
| (567) |
である.一般的に書くと
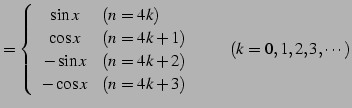 |
(568) |
である.点
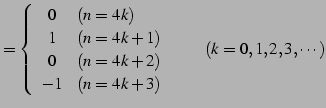 |
(569) |
と求まる. これを用いてテーラー級数を求めると
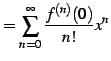 |
(570) | |
| (571) | ||
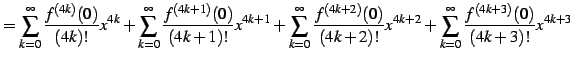 |
(572) | |
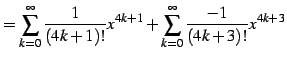 |
(573) | |
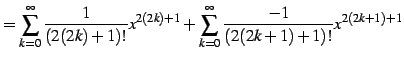 |
(574) | |
| (575) | ||
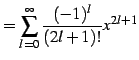 |
(576) | |
| (577) | ||
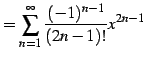 |
(578) |
を得る. 収束半径を求める.
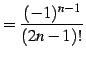 |
(579) |
とおくと
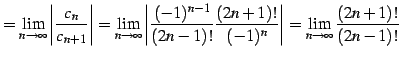 |
(580) | |
| (581) |
が得られる.
例 5.11 (対数関数のテイラー級数)
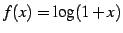 とおく.
導関数を計算すると
とおく.
導関数を計算すると
となる.一般的には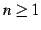 に対して
に対して
と表わされる. 点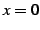 における微分係数は
における微分係数は
となる. よってテーラー級数は
と得られる. 収束半径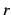 を求める.
を求める.
とおくと,
と得られる.
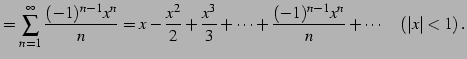 |
(582) |
(導出)
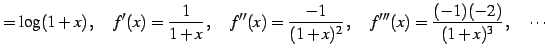 |
(583) |
となる.一般的には
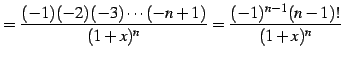 |
(584) |
と表わされる. 点
| (585) |
となる. よってテーラー級数は
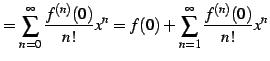 |
(586) | |
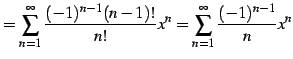 |
(587) |
と得られる. 収束半径
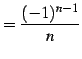 |
(588) |
とおくと,
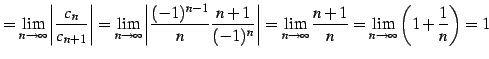 |
(589) |
と得られる.
例 5.12 (有理関数のテイラー級数)
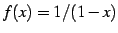 とおく.
導関数を計算すると
とおく.
導関数を計算すると
である. 一般的には
と表わされる. 点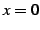 における微分係数は
における微分係数は
と得られる. よってテーラー級数は
となる. 収束半径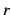 は
は 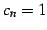 とおくと
とおくと
と得られる.
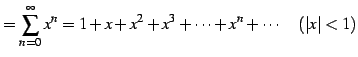 |
(590) |
(導出)
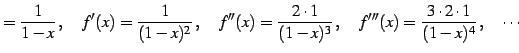 |
(591) |
である. 一般的には
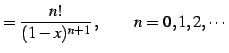 |
(592) |
と表わされる. 点
| (593) |
と得られる. よってテーラー級数は
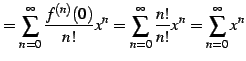 |
(594) |
となる. 収束半径
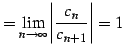 |
(595) |
と得られる.
例 5.13 (多項式のテイラー級数)
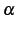 が自然数以外の実数のとき,
が自然数以外の実数のとき,
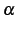 が自然数のとき,
が自然数のとき,
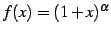 とおく.
導関数を計算すると
とおく.
導関数を計算すると
である.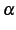 が自然数の場合と,
それ以外の場合に分けて考える.
まず
が自然数の場合と,
それ以外の場合に分けて考える.
まず 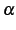 が自然数以外の実数のときを考える.
導関数は
が自然数以外の実数のときを考える.
導関数は
と表わされる. 点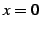 における微分係数は
における微分係数は
となる. よってテーラー級数は
と求まる. 収束半径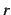 は
は
とおくと,
と得られる. 次に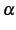 が自然数のときを考える.
導関数は
が自然数のときを考える.
導関数は
と表わされる. 点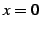 における微分係数は
における微分係数は
と求まる. よってテーラー級数は
と得られる. この展開式は有限項の和であり,有限次数の多項式である.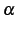 が自然数のときのテーラー展開は
二項展開となる.
展開式は多項式であり任意の実数
が自然数のときのテーラー展開は
二項展開となる.
展開式は多項式であり任意の実数 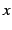 に対して成立する.
よって
に対して成立する.
よって
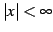 であり,収束半径は
であり,収束半径は 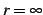 となる.
となる.
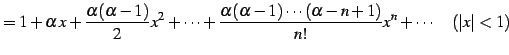 |
(596) | |
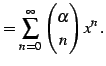 |
(597) |
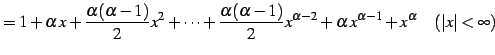 |
(598) | |
 |
(599) |
(導出)
| (600) | ||
| (601) |
である.
| (602) | ||
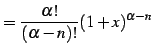 |
(603) |
と表わされる. 点
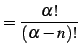 |
(604) |
となる. よってテーラー級数は
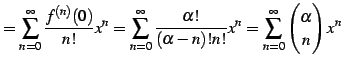 |
(605) |
と求まる. 収束半径
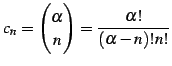 |
(606) |
とおくと,
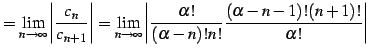 |
(607) | |
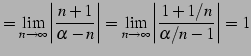 |
(608) |
と得られる. 次に
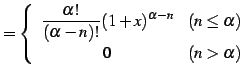 |
(609) |
と表わされる. 点
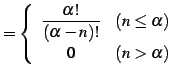 |
(610) |
と求まる. よってテーラー級数は
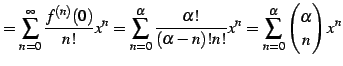 |
(611) |
と得られる. この展開式は有限項の和であり,有限次数の多項式である.
問 5.14
参考書(p.191)問題 7-5 2, 3.
定義 5.15 (階乗の拡張)
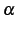 を実数とする.このとき
を実数とする.このとき 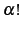 を
を
と定義する.
| (612) |
と定義する.
例 5.16 (階乗の具体例)
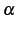 が自然数
が自然数 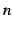 のとき
のとき
である.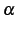 が自然数ではないとき
が自然数ではないとき
となり無限積で表わされる. 例えば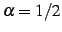 のときは
のときは
となる.
| (613) |
である.
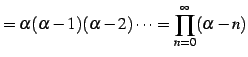 |
(614) |
となり無限積で表わされる. 例えば
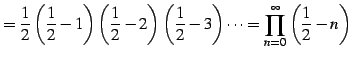 |
(615) | |
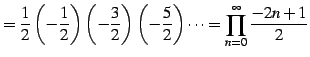 |
(616) |
となる.
定義 5.17 (二項係数の拡張)
実数 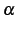 , 自然数
, 自然数 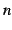 に対して
に対して
と定義する.
 |
(617) |
と定義する.
例 5.18 (二項係数の具体例)
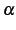 が自然数
が自然数 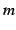 のときは
のときは
であり通常の二項係数と等しい.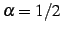 ,
, 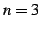 のとき
のとき
となる.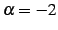 ,
,  のとき
のとき
となる.
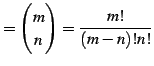 |
(618) |
であり通常の二項係数と等しい.
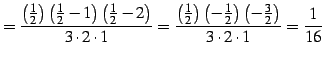 |
(619) |
となる.
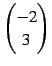 |
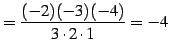 |
(620) |
となる.
注意 5.19 (三角関数と指数関数)
三角関数と指数関数は
の関係にある. ここで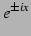 は複素指数関数である.
複素指数関数は複素数
は複素指数関数である.
複素指数関数は複素数 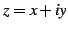 に対して
に対して
と定義される. 右辺は複素巾級数である. この定義より関係式が自然に導出される. このとき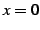 とし
とし 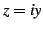 とおく.
すると
とおく.
すると
を得る. 同様に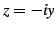 とおくと
とおくと
を得る.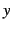 を
を 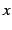 に置き換えることで,最初の関係式を得る.
に置き換えることで,最初の関係式を得る.
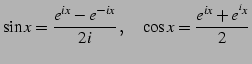 |
(621) |
の関係にある. ここで
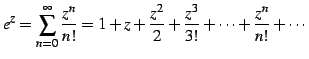 |
(622) |
と定義される. 右辺は複素巾級数である. この定義より関係式が自然に導出される. このとき
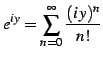 |
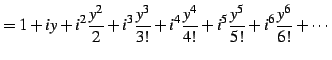 |
(623) |
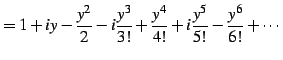 |
(624) | |
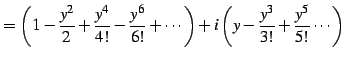 |
(625) | |
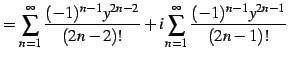 |
(626) | |
| (627) |
を得る. 同様に
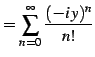 |
(628) | |
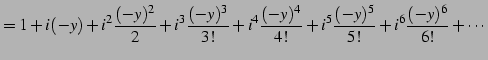 |
(629) | |
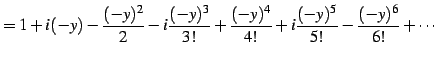 |
(630) | |
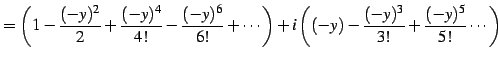 |
(631) | |
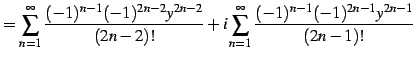 |
(632) | |
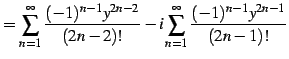 |
(633) | |
| (634) |
を得る.
Next: 5 解析関数 Up: 5 テイラー級数 Previous: 3 テイラー級数の導出 Contents
Kondo Koichi

Created at 2004/08/14