Next: 6 有理関数の積分 Up: 6 積分法 Previous: 4 置換積分法 Contents
5 部分積分法
定理 6.13 (部分積分法)
これを部分積分法(integration by parts)という.
を得る.これを両辺を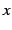 で積分すると
で積分すると
となる.移項すると証明終了.
| (843) |
これを部分積分法(integration by parts)という.
(証明)
関数 ![]() を微分すると積の微分公式より
を微分すると積の微分公式より
| (844) |
を得る.これを両辺を
| (845) |
となる.移項すると証明終了.
例 6.14 (部分積分法の使用例)
| (846) | ||
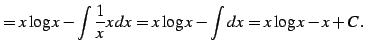 |
(847) |
例 6.15 (部分積分法の使用例)
| (848) | ||
| (849) |
例 6.16 (部分積分法の使用例)
| (850) | ||
| (851) |
Next: 6 有理関数の積分 Up: 6 積分法 Previous: 4 置換積分法 Contents
Kondo Koichi

Created at 2004/08/14