Next: 28 座標変換 Up: 1 ベクトル空間 Previous: 26 直交補空間 Contents
27 基底の変換
ベクトル空間の基底の取り方は一意ではないので,
あるベクトル空間 ![]() に対して
に対して
が成り立つ. ここで
と書ける. ここで
とも表される.
定義 1.123 (基底の変換行列)
ベクトル空間  の基底
の基底
 ,
,
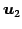 ,
,  ,
,
 と
と
 ,
,
 ,
, 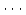 ,
,
 に対して
に対して
をみたす行列 を基底の変換行列という.
を基底の変換行列という.
をみたす行列
定理 1.124 (基底の変換行列の正則性)
基底の変換行列は正則である.
例 1.125 (基底の変換行列の具体例)
を考える. このとき
をみたす基底の変換行列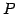 を求める.
標準基底
を求める.
標準基底
 ,
,
 を列ベクトルに並べた行列は
単位行列
を列ベクトルに並べた行列は
単位行列  となるので,
となるので,
を得る.
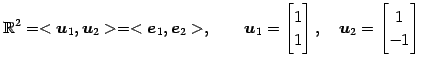 |
を考える. このとき
をみたす基底の変換行列
 |
を得る.
例 1.126 (基底の変換行列の具体例)
を考える. 基底 に対する
に対する
 の変換行列を
の変換行列を  とおく.
つまり,
とおく.
つまり,
をみたす行列 を求める.
まず,標準基底
を求める.
まず,標準基底
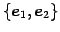 に対する
基底
に対する
基底
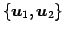 と
と
 の変換行列を
の変換行列を 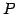 ,
, 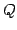 とおく.
すなわち,
とおく.
すなわち,
が成立する.基底の変換行列は正則であるから,
を得る.これらより,
と表される. よって
を得る.
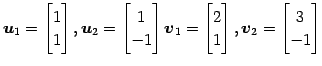 |
を考える. 基底
をみたす行列
が成立する.基底の変換行列は正則であるから,
を得る.これらより,
と表される. よって
 |
を得る.
Next: 28 座標変換 Up: 1 ベクトル空間 Previous: 26 直交補空間 Contents
Kondo Koichi

Created at 2004/12/13