Next: 6 ベクトル空間 Up: 1 ベクトル空間 Previous: 4 体 Contents
5 数ベクトル空間
定義 1.20 (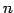 次元実ベクトル空間)
要素が実数の列ベクトル全体の集合
次元実ベクトル空間)
要素が実数の列ベクトル全体の集合
に次の演算が定義されているとき, を
を
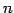 次元実ベクトル空間
(
次元実ベクトル空間
(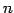 -dimensional real vector space)という.
-dimensional real vector space)という.
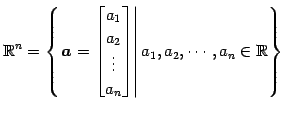 |
に次の演算が定義されているとき,
(i)
ベクトル
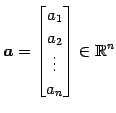 とスカラー
とスカラー
![]() に対して
スカラー倍を次のように定義する:
に対して
スカラー倍を次のように定義する:
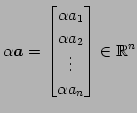 |
(ii) ベクトル
 に対してベクトルの和を
次のように定義する:
に対してベクトルの和を
次のように定義する:
 |
定義 1.21 ( 次元複素ベクトル空間)
要素が複素数の列ベクトル全体の集合
次元複素ベクトル空間)
要素が複素数の列ベクトル全体の集合
に次の演算が定義されているとき,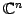 を
を
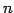 次元複素ベクトル空間
(
次元複素ベクトル空間
( -dimensional complex vector space)という.
-dimensional complex vector space)という.
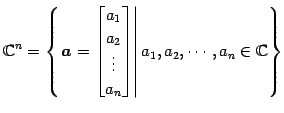 |
に次の演算が定義されているとき,
(i)
ベクトル
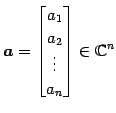 とスカラー
とスカラー
![]() に対して
スカラー倍を次のように定義する:
に対して
スカラー倍を次のように定義する:
 |
(ii) ベクトル
 に対してベクトルの和を
次のように定義する:
に対してベクトルの和を
次のように定義する:
 |
定義 1.22 (数ベクトル空間)
 ,
,
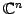 を
数ベクトル空間という.
を
数ベクトル空間という.
注意 1.23 (零ベクトル)
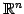 または
または
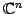 の
零ベクトル(zero vector)を
の
零ベクトル(zero vector)を
と定義する. 零ベクトルは
をみたす.
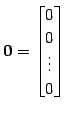 |
と定義する. 零ベクトルは
をみたす.
注意 1.24 (逆ベクトルと差)
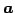 の逆ベクトルを
の逆ベクトルを
と定義する. また, と
と  との差を
との差を
と定義する.
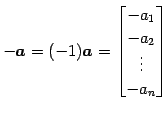 |
と定義する. また,
と定義する.
定理 1.25 (ベクトルの演算の性質)
ベクトル
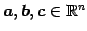 (または
(または
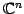 )
とスカラー
)
とスカラー
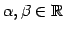 (または
(または
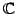 )に対して
次の性質が成立する:
)に対して
次の性質が成立する:
- (i)
- (交換則)
 .
.
- (ii)
- (結合則)
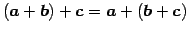 .
.
- (iii)
- (スカラー倍に関する結合則)
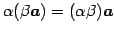 .
.
- (iv)
- (スカラー倍に関する分配即)
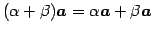 .
.
- (v)
- (スカラー倍に関する分配即)
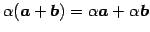 .
.
問 1.26 (ベクトルの演算の性質)
この定理をスカラー倍とベクトルの和の定義を用いて証明せよ.
Next: 6 ベクトル空間 Up: 1 ベクトル空間 Previous: 4 体 Contents
Kondo Koichi

Created at 2004/12/13