Next: 7 内積 Up: 1 ベクトル空間 Previous: 5 数ベクトル空間 Contents
6 ベクトル空間
定義 1.27 (ベクトル空間)
集合 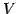 の任意の元
の任意の元 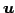 ,
, 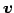 と体
と体 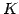 (
(
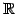 や
や
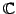 など)の任意の元
など)の任意の元 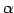 に対して,
和
に対して,
和
とスカラー倍
が定義されていて, 次の性質(i)-(viii)をみたすならば,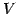 を
を 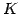 上のベクトル空間(vector space)と呼び,
上のベクトル空間(vector space)と呼び,
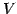 の元
の元
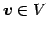 をベクトル(vector)と呼ぶ.
をベクトル(vector)と呼ぶ.
| (9) |
とスカラー倍
| (10) |
が定義されていて, 次の性質(i)-(viii)をみたすならば,
- (i)
- (交換則)
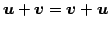 .
.
- (ii)
- (結合則)
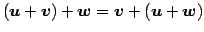 .
.
- (iii)
- (零元の存在)
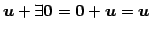 .
.
- (iv)
- (スカラー倍に関する結合則)
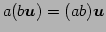 .
.
- (v)
- (スカラー倍に関する分配即)
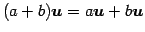 .
.
- (vi)
- (スカラー倍に関する分配即)
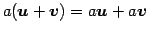 .
.
- (vii)
- (スカラー倍に関する単位元)
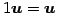 .
.
- (viii)
- (スカラー倍に関する零元)
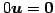 .
.
例 1.28 (ベクトル空間の例)
- 実列ベクトル全体の集合:
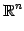
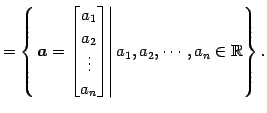
条件(1)-(8)をみたすので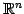 は
は
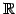 上のベクトル空間である.
上のベクトル空間である.
- 複素列ベクトル全体の集合:
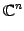
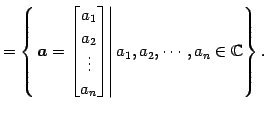
条件(1)-(8)をみたすので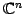 は
は
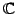 上のベクトル空間である.
上のベクトル空間である.
- 実行ベクトル全体の集合:
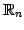
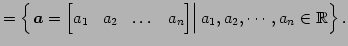
条件(1)-(8)をみたすので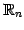 は
は
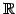 上のベクトル空間である.
上のベクトル空間である.
- 複素行ベクトル全体の集合:
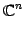
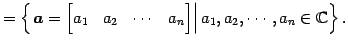
条件(1)-(8)をみたすので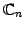 は
は
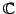 上のベクトル空間である.
上のベクトル空間である.
- 高々
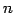 次の実係数多項式全体の集合:
次の実係数多項式全体の集合:
![$\displaystyle \mathbb{R}[x]_{n}$](img256.png)
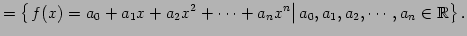
![$ \mathbb{R}[x]_n$](img258.png) の元は多項式であり
の元は多項式であり
![$\displaystyle \mathbb{R}[x]_n\ni f(x)=a_{0}+a_{1}x+a_{2}x^2+\cdots+a_{n}x^{n},$](img259.png)
![$\displaystyle \mathbb{R}[x]_n\ni g(x)=b_{0}+b_{1}x+b_{2}x^2+\cdots+b_{n}x^{n}$](img260.png)
と表される.これらの和は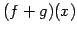
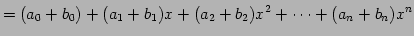
![$\displaystyle = c_{0}+c_{1}x+c_{2}x^2+\cdots+c_{n}x^{n} \in\mathbb{R}[x]_n$](img263.png)
となり,スカラー倍は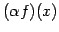
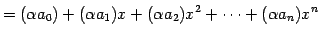
![$\displaystyle = c_{0}+c_{1}x+c_{2}x^2+\cdots+c_{n}x^{n} \in\mathbb{R}[x]_n$](img266.png)
となる.![$ \mathbb{R}[x]_n$](img267.png) は和とスカラー倍の演算について閉じている.
また,
条件(1)-(8)をみたすので,
は和とスカラー倍の演算について閉じている.
また,
条件(1)-(8)をみたすので,
![$ \mathbb{R}[x]_n$](img268.png) は
は
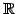 上のベクトル空間である.
上のベクトル空間である.
- 区間
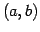 で連続な関数全体の集合:
で連続な関数全体の集合: 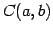 .
.
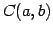 の元は関数であり
の元は関数であり
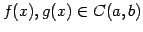 とおく.
これらの和は
とおく.
これらの和は
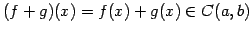
であり連続関数となる. スカラー倍は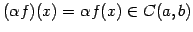
であり連続関数となる.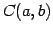 は和とスカラー倍に関して閉じている.
また,条件(1)-(8)をみたすので,
は和とスカラー倍に関して閉じている.
また,条件(1)-(8)をみたすので,
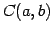 は
は
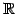 上のベクトル空間である.
上のベクトル空間である.
Next: 7 内積 Up: 1 ベクトル空間 Previous: 5 数ベクトル空間 Contents
Kondo Koichi

Created at 2004/12/13