6.5 部分積分法
定理 6.14 (部分積分法)
これを部分積分法(integration by parts)という.
を得る.これを両辺を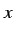 で積分すると
で積分すると
となる.移項すると証明終了.
 |
(881) |
これを部分積分法(integration by parts)という.
(証明)
関数 ![]() を微分すると積の微分公式より
を微分すると積の微分公式より
| (882) |
を得る.これを両辺を
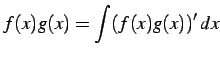 |
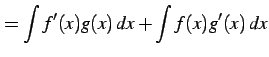 |
(883) |
となる.移項すると証明終了.
例 6.15 (部分積分法の使用例)
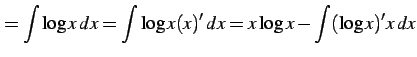 |
(884) | |
 |
(885) |
例 6.16 (部分積分法の使用例)
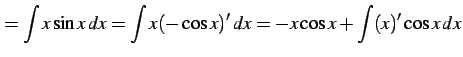 |
(886) | |
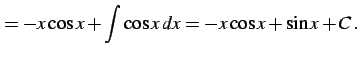 |
(887) |
例 6.17 (部分積分法の使用例)
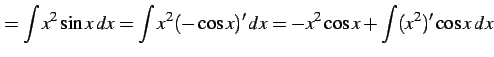 |
(888) | |
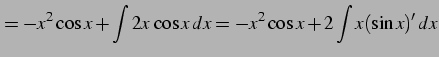 |
(889) | |
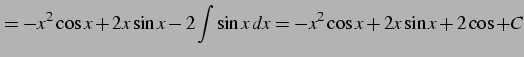 |
(890) | |
| (891) |
Kondo Koichi

平成17年8月31日