6.6 有理関数の積分
有理関数
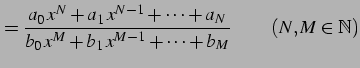 |
(892) |
の不定積分
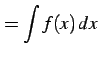 |
(893) |
を考える. 任意の有理関数は積分可能である.
Step 1 (分子を分母で割る)
分子の次数 ![]() が分母の次数
が分母の次数 ![]() 以上のときは
まず割り算を行い,
以上のときは
まず割り算を行い,
 |
(894) |
とする. このとき多項式の部分は必ず積分が可能である. よって以後では分子の次数
Step 2 (分母を因数分解する)
有理式を
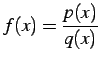 とする.
分母の多項式
とする.
分母の多項式 ![]() を実数の範囲で因数分解する.
このとき
を実数の範囲で因数分解する.
このとき
| (895) |
と表される.
Step 3 (部分分数分解する)
有理式
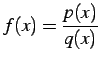 を
部分分数分解する.
すなわち
を
部分分数分解する.
すなわち
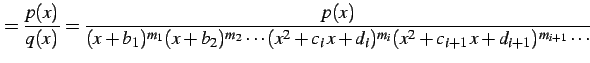 |
(896) | |
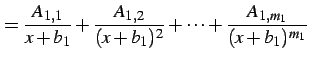 |
(897) | |
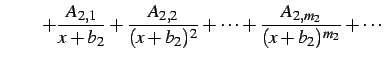 |
(898) | |
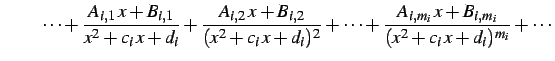 |
(899) |
と変形する.
問 6.18 (部分分数分解)
任意の有理式
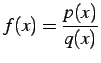
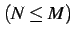 は
上式のように部分分数分解される.これを示せ.
は
上式のように部分分数分解される.これを示せ.
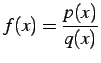
Step 4 (部分分数ごとに積分する)
部分分数ごとに積分を行う.
すなわち
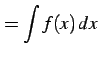 |
(900) | |
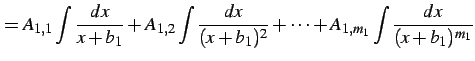 |
(901) | |
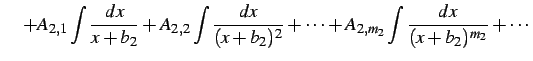 |
(902) | |
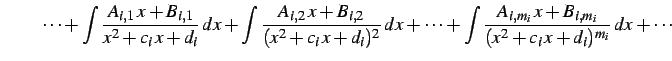 |
(903) |
を計算する. それぞれの場合ごとに積分を考える.
まず,
分母の因子が ![]() 次式の場合の積分を行なう.
すると
次式の場合の積分を行なう.
すると
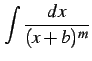 |
![$\displaystyle = \left\{ \begin{array}{ll} \log\vert x+b\vert+C & (m=1)\\ [2ex] \displaystyle{\frac{-1}{m-1}\frac{1}{(x+b)^{m-1}}+C} & (m\ge2) \end{array}\right.$](img1825.png) |
(904) |
を得る.
次に,
分母の因子が ![]() 次式の場合の積分を行なう.
次式の場合の積分を行なう.
![]() 次式の判別式が負であることに注意すると
次式の判別式が負であることに注意すると
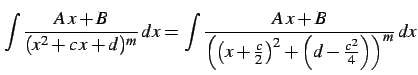 |
(905) |
と表される. ここで
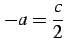 ,
,
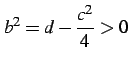 ,
, 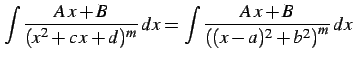 |
(906) |
と表される.この形から積分を進める. さらに式変形すると
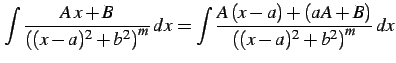 |
(907) | |
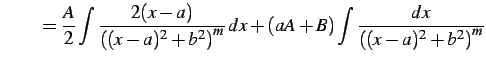 |
(908) | |
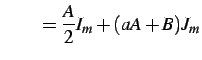 |
(909) |
となる. ここで
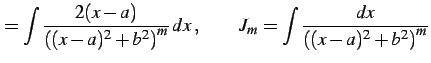 |
(910) |
とおく. 第一項目の積分
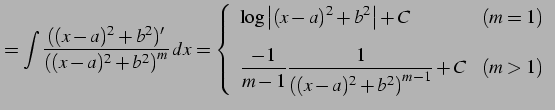 |
(911) |
と求まる. 第二項目の積分
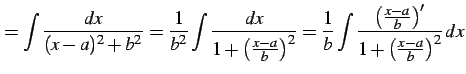 |
(912) | |
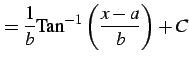 |
(913) |
となる.
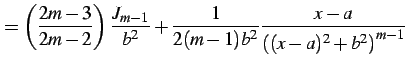 |
(914) |
より
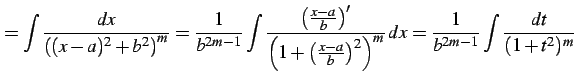 |
(915) |
となる.ここで
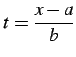 とおいた.
式変形すると
とおいた.
式変形すると
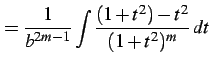 |
(916) | |
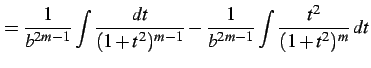 |
(917) | |
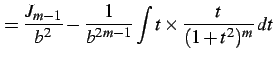 |
(918) | |
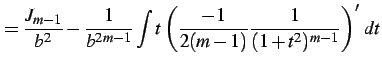 |
(919) | |
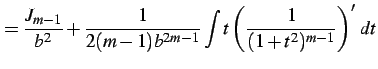 |
(920) | |
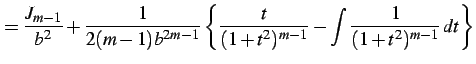 |
(921) | |
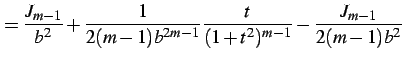 |
(922) | |
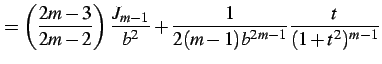 |
(923) | |
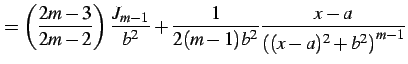 |
(924) |
となり漸化式を得る.
例 6.19 (分母の因数分解)
| (925) | ||
| (926) | ||
| (927) |
例 6.20 (部分分数展開の具体例)
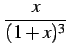 |
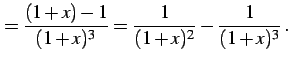 |
(928) |
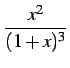 |
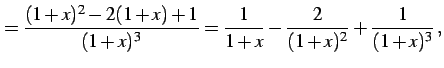 |
(929) |
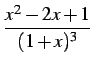 |
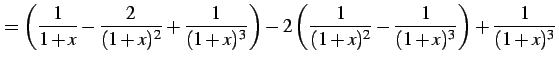 |
(930) |
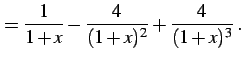 |
(931) |
問 6.21 (部分分数展開の計算例)
部分分数分解として
とする. 係数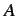 ,
, 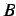 ,
, 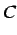 ,
, 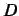 を定めよ.
を定めよ.
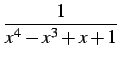 |
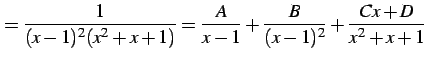 |
(932) |
とする. 係数
問 6.22 (部分分数展開の計算例)
部分分数分解として
とする. 係数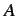 ,
, 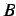 ,
, 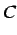 ,
, 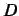 ,
, 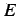 ,
, 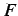 ,
, 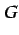 ,
, 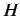 を定めよ.
を定めよ.
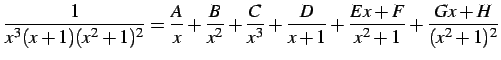 |
(933) |
とする. 係数
例 6.23 (有理式関数の不定積分の具体例)
不定積分
を計算する. 分子の次数が分母の次数以上であるから, 分子を分母で割り
のように変形する. 多項式部分は積分される. 残るは有理式の積分である. これを計算すると
となる. よって
を得る.
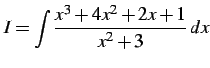 |
(934) |
を計算する. 分子の次数が分母の次数以上であるから, 分子を分母で割り
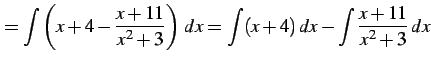 |
(935) | |
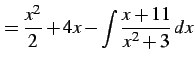 |
(936) |
のように変形する. 多項式部分は積分される. 残るは有理式の積分である. これを計算すると
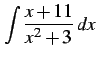 |
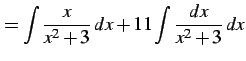 |
(937) |
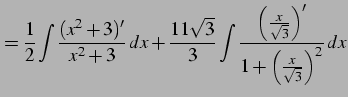 |
(938) | |
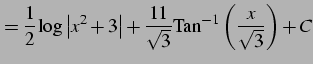 |
(939) |
となる. よって
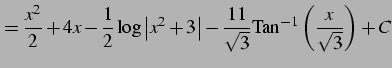 |
(940) |
を得る.
例 6.24 (有理式関数の不定積分の具体例)
不定積分
を計算する.まず, 部分分数分解として
とする. 通分して同じ次数でまとめると
となる.よって係数は
を満足しなければならない. これを解くと
となる. よって部分分数分解は
と表される. よって,
を得る.
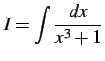 |
(941) |
を計算する.まず, 部分分数分解として
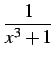 |
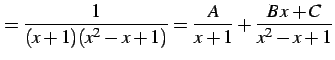 |
(942) |
とする. 通分して同じ次数でまとめると
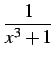 |
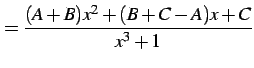 |
(943) |
となる.よって係数は
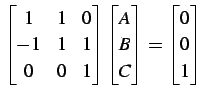 |
(944) |
を満足しなければならない. これを解くと
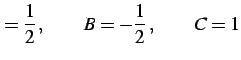 |
(945) |
となる. よって部分分数分解は
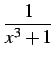 |
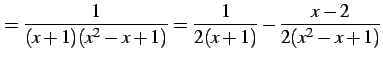 |
(946) |
と表される. よって,
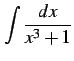 |
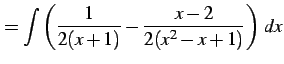 |
(947) |
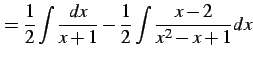 |
(948) | |
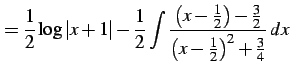 |
(949) | |
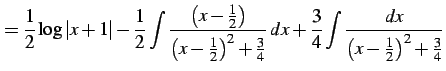 |
(950) | |
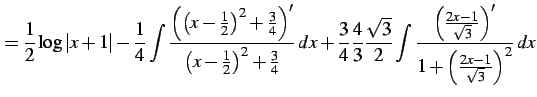 |
(951) | |
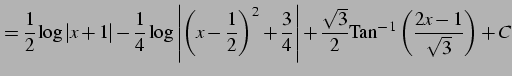 |
(952) | |
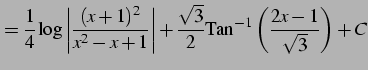 |
(953) |
を得る.
例 6.25 (有理式関数の不定積分の具体例)
不定積分
を計算する. まず,部分分数分解する.
とおくと,
であり,これを解くと
となる.よって
を得る. これを積分して
を得る.
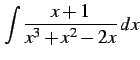 |
(954) |
を計算する. まず,部分分数分解する.
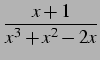 |
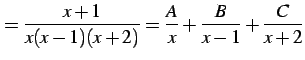 |
(955) |
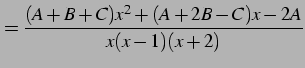 |
(956) |
とおくと,
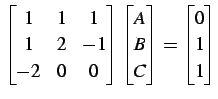 |
(957) |
であり,これを解くと
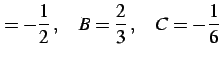 |
(958) |
となる.よって
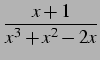 |
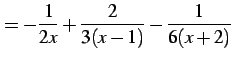 |
(959) |
を得る. これを積分して
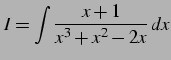 |
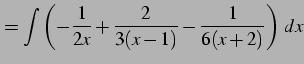 |
(960) |
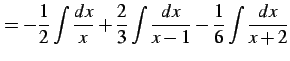 |
(961) | |
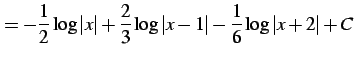 |
(962) | |
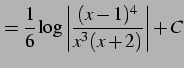 |
(963) |
を得る.
例 6.26 (有理式関数の不定積分の具体例)
不定積分
を計算する. まず
とおくと
より
が定まる.よって
となる.これより
を得る.
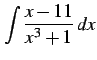 |
(964) |
を計算する. まず
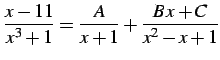 |
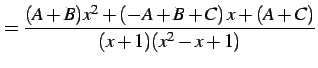 |
(965) |
とおくと
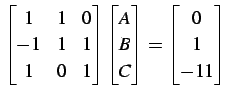 |
(966) |
より
| (967) |
が定まる.よって
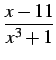 |
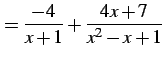 |
(968) |
となる.これより
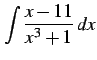 |
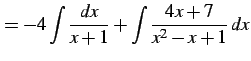 |
(969) |
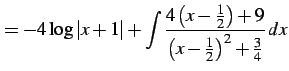 |
(970) | |
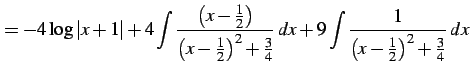 |
(971) | |
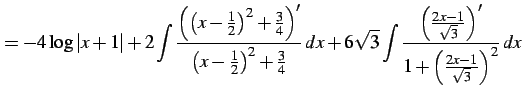 |
(972) | |
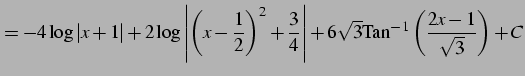 |
(973) | |
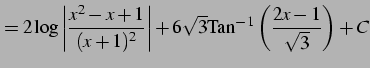 |
(974) |
を得る.
例 6.27 (有理式関数の不定積分の具体例)
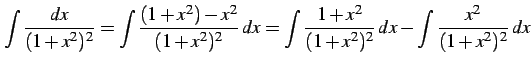 |
(975) | |
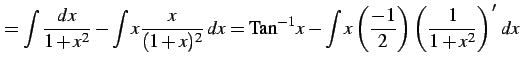 |
(976) | |
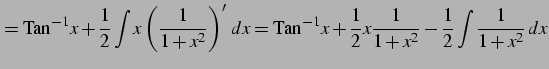 |
(977) | |
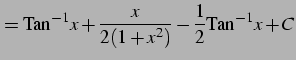 |
(978) | |
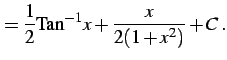 |
(979) |
Kondo Koichi

平成17年8月31日