6.7 根号を含む関数の積分

関数 $f(x)$ に根号 $\sqrt[n]{ax+b}$ $(a\neq0)$ を含む場合の 不定積分を考える． 変数変換

$$t=\sqrt[n]{ax+b}$$ (980)

とおき置換積分法で求積する． 両辺を $n$ 乗すると

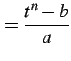$$x = \frac{t^n-b}{a}$$ (981)

を得る．またこれより

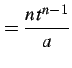$$\frac{dx}{dt} = \frac{n\,t^{n-1}}{a}$$ (982)

が成り立つ．よって $f(x)$ の不定積分は

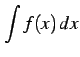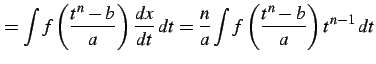$$\int f(x)\,dx = \int f\left(\frac{t^n-b}{a}\right) \frac{dx}{dt}\,dt= \frac{n}{a} \int f\left(\frac{t^n-b}{a}\right)t^{n-1}\,dt$$ (983)

より求められる．

例 6.28 (根号を含む場合の計算例)   不定積分

$$I = \int\frac{dx}{x+2\sqrt{x-1}}$$ (984)

を考える．まず

$$t =\sqrt{x-1}$$ (985)

とおく．これより

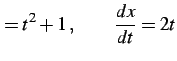$$x =t^2+1\,,\qquad \frac{dx}{dt}=2t$$ (986)

となる．よって置換積分法より

$$I = \int\frac{dx}{x+2\sqrt{x-1}}\,dt= \int\frac{1}{(t^2+1)+2t}\times (2t)\,dt= 2\int\frac{t}{(t+1)^2}\,dt$$ (987)

$$= 2\int\frac{(t+1)-1}{(t+1)^2}\,dt= 2\int\frac{dt}{t+1}-2\int\frac{dt}{(t+1)^2}$$ (988)

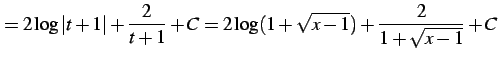$$= 2\log\vert t+1\vert+\frac{2}{t+1}+C= 2\log(1+\sqrt{x-1})+\frac{2}{1+\sqrt{x-1}}+C$$ (989)

を得る．

関数 $f(x)$ に $\sqrt{ax^2+bx+c}$ $(a>0)$ を 含む場合を考える． このときまず

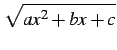$$\sqrt{ax^2+bx+c} =t-\sqrt{a}\,x$$ (990)

とおく．両辺を二乗すれば

$$x = \frac{t^2-c}{b+\sqrt{a}\,t}$$ (991)

を得る．これより

$$\frac{dx}{dt} = \frac{2(\sqrt{a}\,t^2+b\,t+c\sqrt{a})}{(a+2\sqrt{a}\,t)^2}$$ (992)

となる． このとき不定積分は

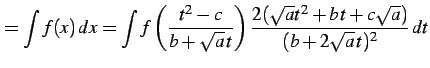$$I =\int f(x)\,dx= \int f\left(\frac{t^2-c}{b+\sqrt{a}\,t}\right) \frac{2(\sqrt{a}t^2+b\,t+c\sqrt{a})}{(b+2\sqrt{a}\,t)^2}\,dt$$ (993)

により求まる．

例 6.29 (根号を含む場合の計算例)   不定積分

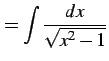$$I =\int\frac{dx}{\sqrt{x^2-1}}$$ (994)

を考える． 変数変換

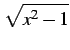$$\sqrt{x^2-1} =t-x$$ (995)

とおく．両辺を二乗すれば

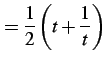$$x = \frac{1}{2} \left( t+\frac{1}{t} \right)$$ (996)

を得る．これより

$$\frac{dx}{dt} = \frac{1}{2}\left(1-\frac{1}{t^2}\right)$$ (997)

となる． よって不定積分は

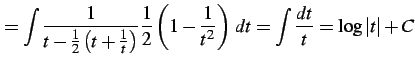$$I = \int\frac{1}{t-\frac{1}{2}\left(t+\frac{1}{t}\right)} \frac{1}{2}\left(1-\frac{1}{t^2}\right)\,dt= \int\frac{dt}{t}= \log\vert t\vert+C$$ (998)

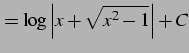$$=\log\left\vert x+\sqrt{x^2-1}\right\vert+C$$ (999)

と求まる．またこの結果は

$$I = \mathrm{Cosh}^{-1}x+C$$ (1000)

とも表される．

例 6.30 (根号を含む場合の計算例)   不定積分

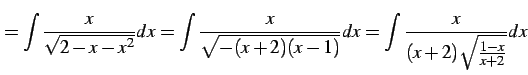$$I =\int\frac{x}{\sqrt{2-x-x^2}}dx= \int\frac{x}{\sqrt{-(x+2)(x-1)}}dx= \int\frac{x}{(x+2)\sqrt{\frac{1-x}{x+2}}}dx$$ (1001)

を求める． 変数変換

$$\sqrt{\frac{1-x}{x+2}}=t$$ (1002)

とおく．このとき

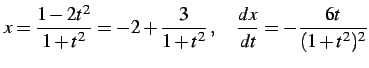$$x=\frac{1-2t^2}{1+t^2}=-2+\frac{3}{1+t^2}\,,\quad \frac{dx}{dt}=-\frac{6t}{(1+t^2)^2}$$ (1003)

である．よって

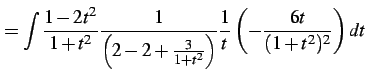$$I = \int\frac{1-2t^2}{1+t^2} \frac{1}{\left(2-2+\frac{3}{1+t^2}\right)}\frac{1}{t} \left(-\frac{6t}{(1+t^2)^2}\right)dt$$ (1004)

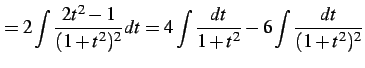$$= 2\int\frac{2t^2-1}{(1+t^2)^2}dt= 4\int\frac{dt}{1+t^2}- 6\int\frac{dt}{(1+t^2)^2}$$ (1005)

Kondo Koichi
平成17年8月31日