6.9 漸化式を用いた積分の計算
例 6.32 (漸化式による不定積分の求積)
不定積分
を考える.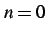 のとき
のとき
を得る. のとき
のとき
を得る. のときを考える.
のときを考える.
 を部分積分を用いて計算すると
を部分積分を用いて計算すると
となる. を移項すると
を移項すると
を得る. 最後の式は漸化式である. この漸化式より不定積分 が求まる.
同様にして
が求まる.
同様にして
を得る.
 |
(1017) |
を考える.
 |
(1018) |
を得る.
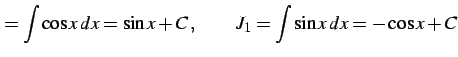 |
(1019) |
を得る.
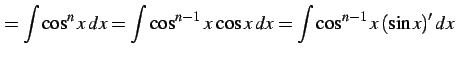 |
(1020) | |
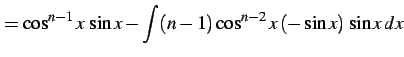 |
(1021) | |
 |
(1022) | |
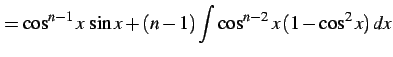 |
(1023) | |
 |
(1024) | |
| (1025) | ||
| (1026) |
となる.
| (1027) | ||
| (1028) | ||
 |
(1029) |
を得る. 最後の式は漸化式である. この漸化式より不定積分
 |
(1030) |
を得る.
問 6.33 (漸化式による不定積分の求積)
 についての漸化式を求めよ.
についての漸化式を求めよ.
注意 6.34 (三角関数の不定積分の計算例)
 ,
,  は
は 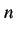 倍角の公式を用いても求積される.
倍角の公式を用いても求積される.
Kondo Koichi

平成17年8月31日