3.17 線積分と多重積分
注意 3.77 (周回積分)
積分路 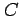 が一周しているとき,
線積分
が一周しているとき,
線積分
 を
を
と表記することがある. これを周回積分とも呼ぶ.
 を
を
 |
と表記することがある. これを周回積分とも呼ぶ.
定義 3.78 (領域の境界)
領域 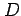 の境界を
の境界を
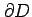 と表記する.
このとき内部が進行方向の左手になるように向きを定める.
(注意)ここで
と表記する.
このとき内部が進行方向の左手になるように向きを定める.
(注意)ここで 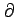 は偏微分の記号とは全く関係ない.
単に記号の形が「ぐるっとまわる」の見えるため.
は偏微分の記号とは全く関係ない.
単に記号の形が「ぐるっとまわる」の見えるため.
 |
 |
| (a) 領域 |
(b) 穴のあいた領域 |
定理 3.79 (グリーンの定理)
領域 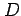 内で関数
内で関数
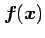 が連続なとき,
が連続なとき,
が成り立つ.
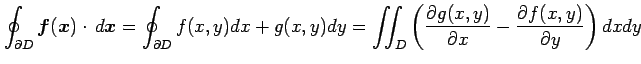 |
が成り立つ.
注意 3.80 (グリーンの定理)
グリーンの定理は線積分と多重積分の移り合いを表す.
例 3.81 (グリーンの定理の使用例)
 を半径
を半径 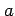 の円上を 1 周する有向曲線
の円上を 1 周する有向曲線
とする. このとき の内部の領域は
の内部の領域は
である. 領域 において関数
において関数 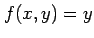 ,
, 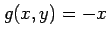 は連続であるから,
線積分
は連続であるから,
線積分
はグリーンの定理が適用でき,
と計算される.
とする. このとき
である. 領域
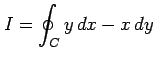 |
はグリーンの定理が適用でき,
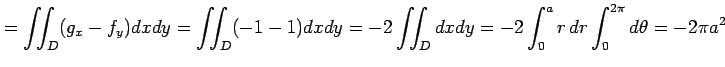 |
と計算される.
例 3.82 (グリーンの定理が使用不可な例)
線積分
を考える.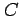 は単位円上を 1 周する有向曲線であり,
は単位円上を 1 周する有向曲線であり,
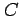 の内部の領域は
の内部の領域は
である. 関数
は原点で連続ではないので, 領域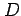 のすべての点において
関数
のすべての点において
関数 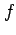 ,
, 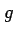 は連続ではないからグリーンの定理は適用できない.
は連続ではないからグリーンの定理は適用できない.
より,
となる. 正しくは,
と得られる.
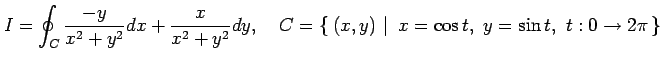 |
を考える.
である. 関数
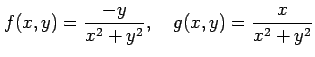 |
は原点で連続ではないので, 領域
誤りではあるが, グリーンの定理を適用して計算すると,
 |
より,
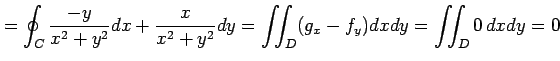 |
となる. 正しくは,
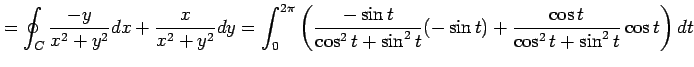 |
||
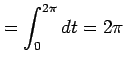 |
と得られる.
Kondo Koichi

平成18年1月18日