3.13 体積の計算
例 3.62 (球の体積)
半径 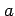 の球の体積は
の球の体積は
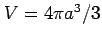 である.
これを多重積分で求める.
である.
これを多重積分で求める.
であり,上面が
の体積
として求める. 2 次元の極座標 ,
,
 とおくと,
領域
とおくと,
領域  と等価な領域は
と等価な領域は
であり,面積素は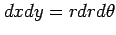 となるので,
となるので,
と得られる.
の体積
として求める. 3 次元の極座標 ,
,
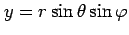 ,
,
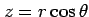 とおくと,
領域
とおくと,
領域  と等価な領域は
と等価な領域は
であり,体積素は
となるので,
と得られる.
(その 1) 球を 8 等分し底面が
であり,上面が
の体積
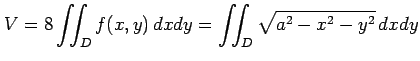 |
として求める. 2 次元の極座標
 |
であり,面積素は
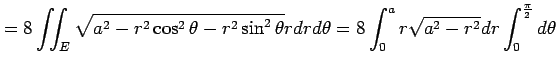 |
||
![$\displaystyle = 8\left[\vrule height1.5em width0em depth0.1em\,{\frac{2}{3(-2)}...
...a}\,\right]_{0}^{\frac{\pi}{2}}= \frac{8a^3}{3}\frac{\pi}{2}= \frac{4\pi}{3}a^3$](img1931.png) |
と得られる.
(その 2) 球を 8 等分し,領域
の体積
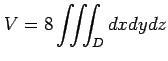 |
として求める. 3 次元の極座標
 |
であり,体積素は
となるので,
![$\displaystyle =8\iiint_Er^2\sin\theta\,drd\theta d\varphi= 8 \int_0^a r^2\,dr \...
...ft[\vrule height1.5em width0em depth0.1em\,{\varphi}\,\right]_0^{\frac{\pi}{2}}$](img1934.png) |
||
 |
と得られる.
例 3.63 (円柱の体積)
底面の半径 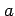 ,高さ
,高さ  の円柱の体積は
の円柱の体積は
 である.
これを多重積分で求める.
である.
これを多重積分で求める.
とおく.円柱の上面は平面 である.
円柱の体積は
である.
円柱の体積は
と求まる. ただし,
とする.
と表される. この領域を円筒座標 ,
,
 ,
,  で置き換えると,
で置き換えると,
 の領域は
の領域は
であり,ヤコビアンは
であるので,
が成り立つ. 円柱の体積は
と求まる.
(その 1)
円柱の底面が ![]() 平面にあるとし,
平面にあるとし,
とおく.円柱の上面は平面
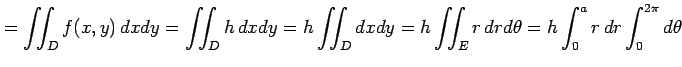 |
||
![$\displaystyle = h\left[\vrule height1.5em width0em depth0.1em\,{\frac{r^2}{2}}\...
...eft[\vrule height1.5em width0em depth0.1em\,{\theta}\,\right]_0^{2\pi}=\pi a^2h$](img1939.png) |
と求まる. ただし,
とする.
(その 2) 円柱の領域は
と表される. この領域を円筒座標
であり,ヤコビアンは
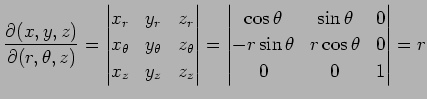 |
であるので,
が成り立つ. 円柱の体積は
![$\displaystyle = \iiint_{D}dxdyz= \iiint_{E}rdrd\theta dz= \int_0^{a}r\,dr\int_0...
...imes \left[\vrule height1.5em width0em depth0.1em\,{z}\,\right]_0^{h}= \pi a^2h$](img1947.png) |
と求まる.
![\includegraphics[width=0.5\textwidth]{taiseki-enchu.eps}](img1948.png)
例 3.64 (円錐の体積)
底面の半径 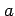 ,高さ
,高さ  の円錐の体積は
の円錐の体積は
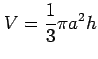 である.
これを多重積分で求める.
円錐の底面は
である.
これを多重積分で求める.
円錐の底面は  平面にあるとし,
その領域を
平面にあるとし,
その領域を
とおく.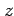 軸と点
軸と点  との距離を
との距離を
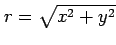 とおくと,
円錐の斜面では図 (b) より,
とおくと,
円錐の斜面では図 (b) より,
が成り立つ.よって,斜面は
と表される.よって円錐の体積は
と求まる. ただし,極座標変換を用いて
とした.
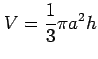 である.
これを多重積分で求める.
円錐の底面は
である.
これを多重積分で求める.
円錐の底面は とおく.
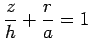 |
が成り立つ.よって,斜面は
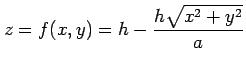 |
と表される.よって円錐の体積は
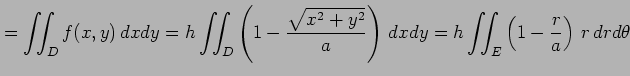 |
||
![$\displaystyle = h\int_0^a\left(r-\frac{r^2}{a}\right)dr\int_0^{2\pi}d\theta= h\...
...ight1.5em width0em depth0.1em\,{\theta}\,\right]_0^{2\pi} = \frac{1}{3}\pi a^2h$](img1954.png) |
と求まる. ただし,極座標変換を用いて
とした.
問 3.65 (円錐の体積)
円錐の体積を
により求めよ.
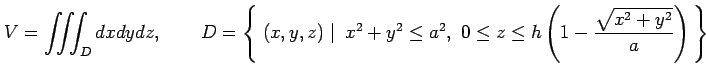 |
により求めよ.
![\includegraphics[width=0.5\textwidth]{taiseki-ensui.eps}](img1956.png) |
![\includegraphics[width=0.3\textwidth]{taiseki-ensui-rz.eps}](img1957.png) |
| (a) 円錐 | (b) |
例 3.66 (体積の計算)
半球
と無限にのびる円柱
の共通部分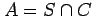 の体積
の体積  を求める.
領域
を求める.
領域 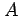 は
は
と表される. 領域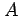 は底面の領域を
は底面の領域を
とする曲面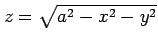 の体積であるから,
の体積であるから,
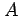 の体積
の体積  は
は
と求まる. ここで 2 次元の極座標 ,
,
 を用いた.
領域は
を用いた.
領域は  は領域
は領域  と等価な領域で
と等価な領域で
である.
と無限にのびる円柱
の共通部分
と表される. 領域
とする曲面
 |
||
 |
||
![$\displaystyle = \frac{2a^3}{3} \int_{0}^{\frac{\pi}{2}} (1-\sin\theta+\sin\thet...
...3\theta}\,\right]_0^{\frac{\pi}{2}} = \left(\frac{\pi}{3}-\frac{4}{9}\right)a^3$](img1967.png) |
と求まる. ここで 2 次元の極座標
 |
である.
![\includegraphics[width=0.6\textwidth]{taiseki-kyu-enchu.eps}](img1969.png) |
![\includegraphics[width=0.4\textwidth]{taiseki-kyu-enchu-theta.eps}](img1970.png) |
| (a) |
(b) 領域 |
例 3.67 (体積の計算)
球
と円柱
の共通部分 を球
を球  から取り除いた領域
から取り除いた領域
 の体積
の体積  を求める.
領域
を求める.
領域 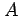 を 8 等分して体積を
を 8 等分して体積を
により求める. 2 次元の極座標変換をすると底面の領域 は
は
であり,体積は
と求まる.
と円柱
の共通部分
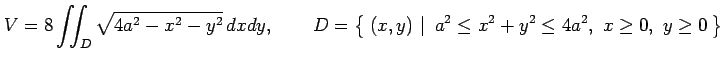 |
により求める. 2 次元の極座標変換をすると底面の領域
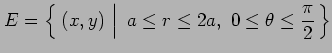 |
であり,体積は
 |
||
![$\displaystyle =8 \left[\vrule height1.5em width0em depth0.1em\,{\theta}\,\right...
...}}}\,\right]_{a}^{2a}= 8\frac{\pi}{2}\frac{(\sqrt{3}a)^3}{3} = 4\sqrt{3}\pi a^3$](img1979.png) |
と求まる.
例 3.68 (体積の計算)
領域
の体積を求める. この領域の 平面の底面の領域は
平面の底面の領域は
であり,上面は平面となり, で表される.
よって,体積は
で表される.
よって,体積は
と得られる.
の体積を求める. この領域の
であり,上面は平面となり,
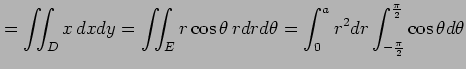 |
||
![$\displaystyle =\left[\vrule height1.5em width0em depth0.1em\,{\frac{r^3}{3}}\,\...
...th0.1em\,{\sin\theta}\,\right]_{-\frac{\pi}{2}}^{\frac{\pi}{2}}= \frac{2a^3}{3}$](img1984.png) |
と得られる.
問 3.69 (体積の計算)
2 つの円柱
の共通部分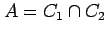 の体積
の体積  を求めよ.
を求めよ.
の共通部分
Kondo Koichi

平成19年1月23日