1.11 内積
定義 1.57 (内積)
![$ \mathbb{R}^{n}\ni\vec{a}=
\begin{bmatrix}{a_{1}}\\ [-.5ex]{a_{2}}\\ [-.5ex]{\vdots}\\ [-.5ex]{a_{n}}\end{bmatrix}$](img333.png) ,
,
![$ \vec{b}=
\begin{bmatrix}{b_{1}}\\ [-.5ex]{b_{2}}\\ [-.5ex]{\vdots}\\ [-.5ex]{b_{n}}\end{bmatrix}$](img334.png) に対して
に対して
なる二項演算を内積(inner product)または スカラー積(scalar product)という. また, に対しては
に対しては
と定義する.
![$ \mathbb{R}^{n}\ni\vec{a}=
\begin{bmatrix}{a_{1}}\\ [-.5ex]{a_{2}}\\ [-.5ex]{\vdots}\\ [-.5ex]{a_{n}}\end{bmatrix}$](img333.png) ,
,
![$ \vec{b}=
\begin{bmatrix}{b_{1}}\\ [-.5ex]{b_{2}}\\ [-.5ex]{\vdots}\\ [-.5ex]{b_{n}}\end{bmatrix}$](img334.png) に対して
に対して
 |
(64) |
なる二項演算を内積(inner product)または スカラー積(scalar product)という. また,
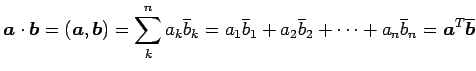 |
(65) |
と定義する.
定義 1.58 (複素数)
複素数(complex number)とは,
実数  に対して
に対して 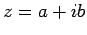 で定まる数である.
ただし
で定まる数である.
ただし 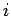 は
は 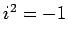 をみたし,
虚数単位(imaginary unit)と呼ぶ.
をみたし,
虚数単位(imaginary unit)と呼ぶ.
 を実部(real part)といい
を実部(real part)といい
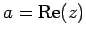 と表す.
と表す.
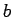 を虚部(imaginary part)といい
を虚部(imaginary part)といい
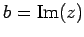 と表す.
虚部が
と表す.
虚部が
 のとき
のとき
 は実数(real number)といい,
実部が
は実数(real number)といい,
実部が
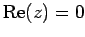 のとき
のとき  は
純虚数(pure imaginary number)という.
複素数全体の集合を
は
純虚数(pure imaginary number)という.
複素数全体の集合を
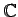 と表す.
実部
と表す.
実部
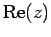 を横軸に虚部
を横軸に虚部
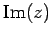 を縦軸にとることできる
集合
を縦軸にとることできる
集合
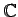 の平面を複素平面(complex plane)と呼ぶ.
複素平面の横軸を実軸(real axis)といい,
縦軸を虚軸(imaginary axis)という.
また,複素数
の平面を複素平面(complex plane)と呼ぶ.
複素平面の横軸を実軸(real axis)といい,
縦軸を虚軸(imaginary axis)という.
また,複素数 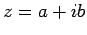 に対して複素数
に対して複素数
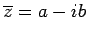 を
を
 の複素共役(complex conjugate)という.
実数
の複素共役(complex conjugate)という.
実数
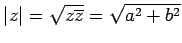 を
を
 の絶対値(absolute value)
または大きさ(modulus)という.
実数
の絶対値(absolute value)
または大きさ(modulus)という.
実数
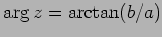 を
を  の
偏角(argument)という.
の
偏角(argument)という.
 は複素平面上で原点 0 と
は複素平面上で原点 0 と  との距離を表し,
との距離を表し,
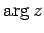 は点 0,
は点 0,  を通る直線と実軸とのなす角を表す.
を通る直線と実軸とのなす角を表す.
定理 1.59 (複素数の性質)
複素数 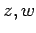 に対して次の性質が成り立つ:
に対して次の性質が成り立つ:
(i)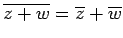 (ii)
(ii)
 (iii)
(iii)
 (iv)
(iv)
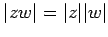
(v)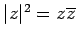 (vi)
(vi)
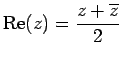 (vii)
(vii)
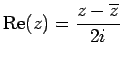 (viii)
(viii)
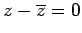
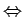
 は実数
は実数
(ix)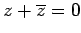
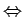
 は純虚数
は純虚数
(i)
(v)
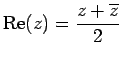 (vii)
(vii)
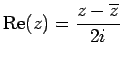 (viii)
(viii)
(ix)
例 1.60 (内積の具体例)
ベクトル
の内積は
である.
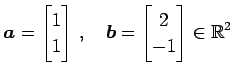 |
(66) |
の内積は
| (67) |
である.
例 1.61 (内積の具体例)
ベクトル
の内積は
である.
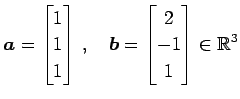 |
(68) |
の内積は
| (69) |
である.
例 1.62 (内積の具体例)
ベクトル
の内積は
である.
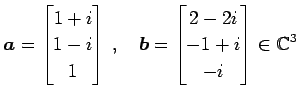 |
(70) |
の内積は
| (71) |
である.
定理 1.63 (内積の性質)
- (i)
-
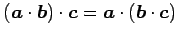 (結合則)
(結合則)
- (ii)
-
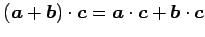 (分配則)
(分配則)
- (iii)
-
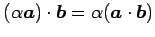 (スカラー倍の結合則)
(スカラー倍の結合則)
- (iv)
-
 (交換則)
(交換則)
- (v)
-
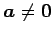 のとき
のとき
 (内積の非負性)
(内積の非負性)
問 1.64 (内積の性質)
これを示せ.
Kondo Koichi
 KONDO Koichi
KONDO Koichi
平成19年1月25日