1.5 ベクトルの成分
定義 1.22 (ベクトルの成分)
ベクトル
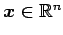 が
が
と表されるとき, 係数の組 を
基本ベクトル
を
基本ベクトル
 ,
,
 ,
,  ,
,
 に関するベクトル
に関するベクトル  の
成分(component)または
座標(coordinate)という.
の
成分(component)または
座標(coordinate)という.
と表されるとき, 係数の組 を
基底
を
基底
 ,
,
 ,
,  ,
,
 に関するベクトル
に関するベクトル  の
成分(component)または
座標(coordinate)という.
の
成分(component)または
座標(coordinate)という.
| (17) |
と表されるとき, 係数の組
また,
![]() の基底(basis)
(座標軸と同じ向きのベクトル)
の基底(basis)
(座標軸と同じ向きのベクトル)
![]() ,
,
![]() ,
, ![]() ,
,
![]() が
与えられているとする.
ベクトル
が
与えられているとする.
ベクトル
![]() が
が
| (18) |
と表されるとき, 係数の組
例 1.23 (ベクトルの成分の具体例)
 空間とその中の点
空間とその中の点
を考える. ただし, ,
,  は基底であり,
は基底であり,
とする. このとき
が成り立つ. ベクトル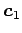 ,
,
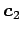 ,
,
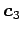 の
基本ベクトル
の
基本ベクトル
に関する成分はそれぞれ ,
,
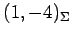 ,
,
 である.
ベクトル
である.
ベクトル
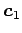 ,
,
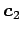 ,
,
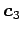 の
基底
の
基底 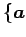 ,
, 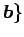 に関する成分は
それぞれ
に関する成分は
それぞれ
 ,
,
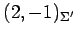 ,
,
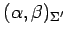 である.
である.
| (19) |
を考える. ただし,
 |
(20) |
とする. このとき
 |
(21) | |
 |
(22) | |
 |
(23) |
が成り立つ. ベクトル
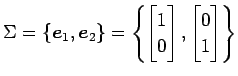 |
(24) |
に関する成分はそれぞれ
これは次のように考える.
![]() の座標軸を
の座標軸を
![]() とする.
これとは別の座標軸として
とする.
これとは別の座標軸として
![]() を導入する.
原点を通り
を導入する.
原点を通り ![]() と同じ向きの座標軸を
と同じ向きの座標軸を ![]() とし,
同様に
とし,
同様に ![]() と同じ向きの座標軸を
と同じ向きの座標軸を ![]() とする.
座標軸
とする.
座標軸 ![]() ,
, ![]() の目盛はそれぞれ
の目盛はそれぞれ
![]() ,
, ![]() の長さを
の長さを ![]() として書く.
このとき点
として書く.
このとき点
![]() ,
,
![]() ,
,
![]() は
座標軸
は
座標軸
![]() 上の座標で表すと
それぞれ
上の座標で表すと
それぞれ
![]() ,
,
![]() ,
,
![]() となる.
となる.
Kondo Koichi
 KONDO Koichi
KONDO Koichi
平成19年1月25日