5.18 テイラー級数による関数の近似
定義 5.44 (関数の近似)
関数  を
テイラー級数
を
テイラー級数
で表わし,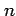 次の項で打ち切った関数
次の項で打ち切った関数
を の
の 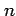 次近似と呼ぶ.
次近似と呼ぶ.
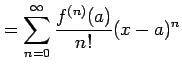 |
で表わし,
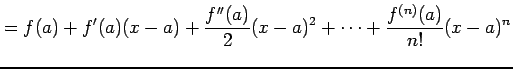 |
を
具体的に書くと
| 0 次近似: | ||
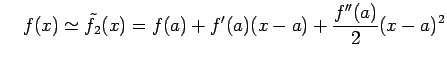 ← 放物線 ← 放物線 |
||
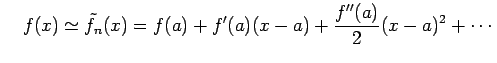 |
||
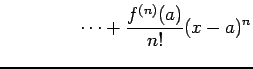 ← ← |
と表される. テイラー級数による関数の近似では
注意 5.45 (関数の近似)
近似式
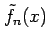 は
曲線
は
曲線 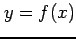 に点
に点 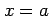 で接する
で接する 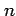 次多項式である.
次多項式である.
例 5.46 (関数の近似の具体例)
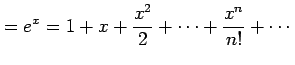 |
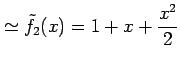 |
||
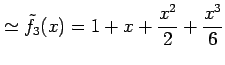 |
例 5.47 (関数の近似の具体例)
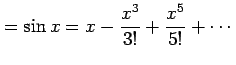 |
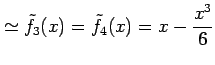 |
||
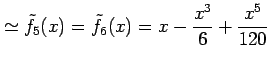 |
平成19年10月3日