5.19 近似関数の誤差の評価
関数 ![]() の
の ![]() 次近似式
次近似式
![]() の誤差
の誤差 ![]() を考える.
テイラー展開
を考える.
テイラー展開
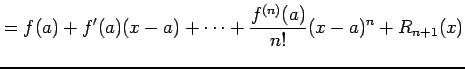 |
より
が成り立つ. 誤差(error)を
と定義すると, 上の式より誤差は
と表される.
例 5.48 (誤差の評価の具体例)
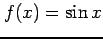 を多項式で近似する.
を多項式で近似する.
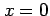 まわりでテイラー展開して近似式を計算すると
まわりでテイラー展開して近似式を計算すると
を得る. 誤差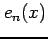 は
は
である. ここで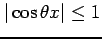 を用いた.
を用いた.
となる.近似の次数が大きいほど誤差は小さい. 次に誤差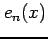 が
が 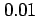 以下となるような
以下となるような 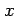 の範囲を求める.
上の誤差の評価式より
の範囲を求める.
上の誤差の評価式より
となる. 近似の次数が上がるほど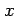 の範囲が広がっている.
の範囲が広がっている.
| 0 次近似: | ||
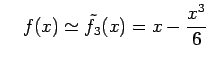 |
||
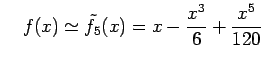 |
を得る. 誤差
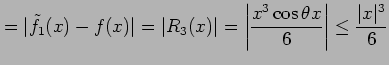 |
||
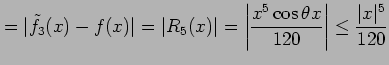 |
||
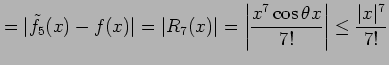 |
である. ここで
いま ![]() のときの誤差を考える.
このとき誤差は
のときの誤差を考える.
このとき誤差は
| 有効桁数: |
||||||||
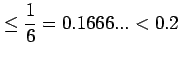 |
有効桁数: |
|||||||
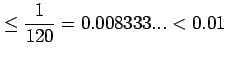 |
有効桁数: |
|||||||
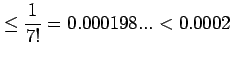 |
有効桁数: |
となる.近似の次数が大きいほど誤差は小さい. 次に誤差
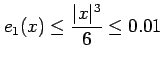 |
||
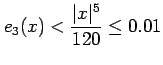 |
||
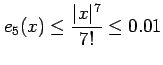 |
となる. 近似の次数が上がるほど
平成19年10月3日