6.19 図形の面積
定理 6.86 (図形の面積)
曲線 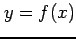 ,
, 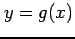 と直線
と直線 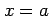 ,
,  とで囲まれてできる領域の
面積は
とで囲まれてできる領域の
面積は
により求まる.
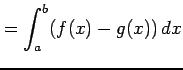 |
により求まる.
定理 6.87 (図形の面積)
曲線 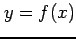 と
と 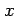 軸 と直線
軸 と直線 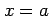 ,
,  で囲まれてできる領域の
面積は
で囲まれてできる領域の
面積は
により求まる.
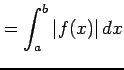 |
により求まる.
例 6.88 (図形の面積の計算例)
単位円 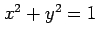 の内部の領域の面積を求める.
円の方程式は書き直すと
の内部の領域の面積を求める.
円の方程式は書き直すと
と表される.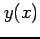 は 2 価関数である.
枝をそれぞれ
は 2 価関数である.
枝をそれぞれ
とおく.このとき円の面積は
と求まる.
と表される.
とおく.このとき円の面積は
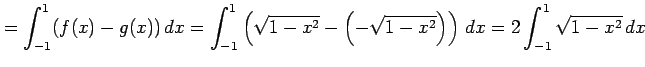 |
||
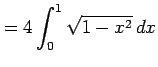 |
||
| ( |
||
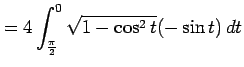 |
||
| (積分区間をひっくり返す.
|
||
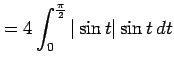 |
||
| (
|
||
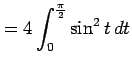 |
||
| (
|
||
![$\displaystyle = 2\int_{0}^{\frac{\pi}{2}}(1-\cos 2t)\,dt= \Big[2t-\sin 2t\Big]_{0}^{\frac{\pi}{2}}= 2\times\frac{\pi}{2}-0-\sin(\pi)+\sin(0)=\pi$](img2793.png) |
と求まる.
例 6.89 (図形の面積の計算例)
曲線 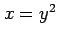 と直線
と直線 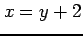 とで囲まれてできる領域の
面積は
とで囲まれてできる領域の
面積は
により求まる.
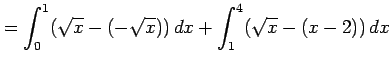 |
により求まる.
例 6.90 (図形の面積の計算例)
円 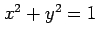 を直線
を直線 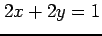 で 2 つに分割する.
分割された上側の領域の面積を求める.
面積は
で 2 つに分割する.
分割された上側の領域の面積を求める.
面積は
により求まる.ここで,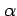 ,
, 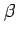 (
(
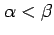 )は
円と直線の交点の
)は
円と直線の交点の 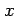 座標で
座標で
の根である. 計算は自習.
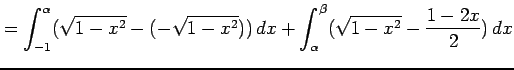 |
により求まる.ここで,
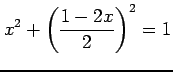 |
の根である. 計算は自習.
平成19年10月3日