6.20 曲線の長さ
定理 6.91 (曲線の長さ)
区間 ![$ [a,b]$](img2663.png) における関数
における関数 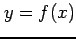 のグラフの曲線の長さは
のグラフの曲線の長さは
により得られる.
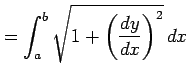 |
により得られる.
注意 6.92 (曲線の長さ)
曲線 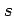 のうちある点
のうちある点 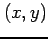 のまわりの微小線分を
のまわりの微小線分を 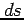 とする.
このとき
とする.
このとき 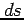 を斜辺とする直角三角形を考える.
その他の辺の長さを
を斜辺とする直角三角形を考える.
その他の辺の長さを 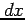 ,
, 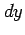 とするとピタゴラスの定理より
とするとピタゴラスの定理より
が成り立つ. 数学的には厳密ではないが次の展開をすると微小線分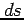 は
は
と表される. 曲線の長さ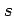 は微小線分
は微小線分 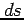 を全て足し合わせたものだから
を全て足し合わせたものだから
となる.
が成り立つ. 数学的には厳密ではないが次の展開をすると微小線分
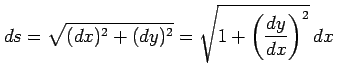 |
と表される. 曲線の長さ
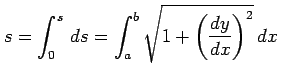 |
となる.
例 6.93 (曲線の長さの計算例)
単位円の円周の長さを考える.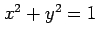 より
より
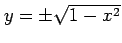 だから
多価関数の枝を分けて
だから
多価関数の枝を分けて
とする.このとき
が成り立つ.よって
を得る.
とする.このとき
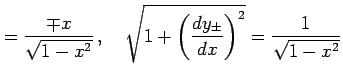 |
が成り立つ.よって
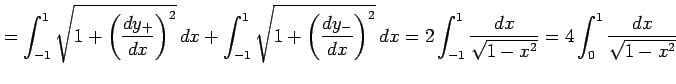 |
||
![$\displaystyle = 4\Big[\mathrm{Sin}^{-1}x\Big]_{0}^{1}= 4\left(\mathrm{Sin}^{-1}(1)-\mathrm{Sin}^{-1}(0)\right)= 4\left(\frac{\pi}{2}-0\right)=2\pi$](img2816.png) |
を得る.
例 6.94 (曲線の長さの計算例)
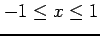 における曲線
における曲線 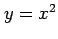 の長さ考える.
の長さ考える.
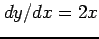 であるから曲線の長さ
であるから曲線の長さ 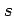 は
は
と表される.積分を計算する.置換積分として
とおく.すると
となる.双曲線関数の性質
を用いると
となる.
を用いると
となる.ここで
であることを用いると
を得る.
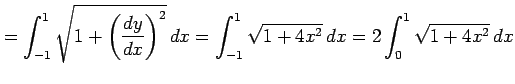 |
と表される.積分を計算する.置換積分として
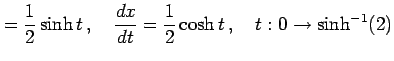 |
とおく.すると
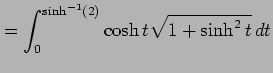 |
となる.双曲線関数の性質
を用いると
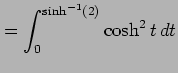 |
となる.
 |
を用いると
![$\displaystyle =\frac{1}{2} \int_{0}^{\sinh^{-1}(2)}(\cosh 2t+1)\,dt= \left[\frac{1}{4}\sinh 2t+\frac{t}{2}\right]_{0}^{\sinh^{-1}(2)}$](img2827.png) |
||
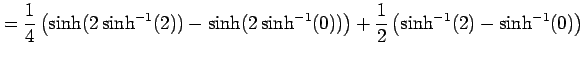 |
||
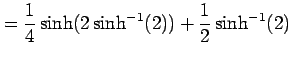 |
となる.ここで
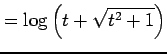 |
であることを用いると
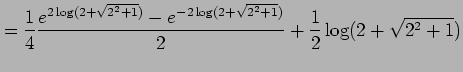 |
||
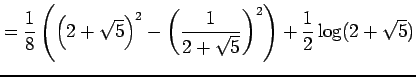 |
||
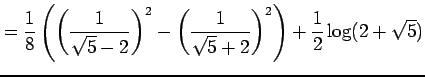 |
||
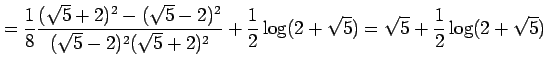 |
を得る.
例 6.95 (曲線の長さの計算例)
前例題において
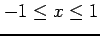 における曲線
における曲線 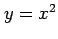 の長さは
の長さは
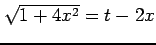 とおいて置換積分すると
とおいて置換積分すると
と表される.
![$\displaystyle = \int_{0}^{1}\sqrt{1+4x^2}\,dx= \frac{1}{8} \int_{1}^{2+\sqrt{5}...
...em depth0.1em\,{\frac{t^2}{2}+2\log t-\frac{1}{2t^2}}\,\right]_{1}^{2+\sqrt{5}}$](img2838.png) |
||
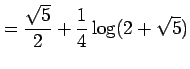 |
と表される.
例 6.96 (曲線の長さの計算例)
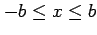 における曲線
における曲線
の長さ考える. これはひもをつるしたとき重力でたわんでできるひもの曲線の形を表しており, 懸垂線(けんすいせん)という. これを計算する.まず,
より,曲線の長さ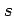 は
は
と表される.
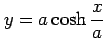 |
の長さ考える. これはひもをつるしたとき重力でたわんでできるひもの曲線の形を表しており, 懸垂線(けんすいせん)という. これを計算する.まず,
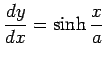 |
より,曲線の長さ
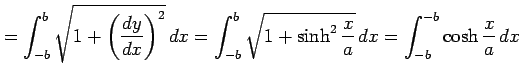 |
||
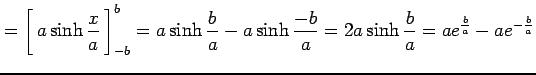 |
と表される.
平成19年10月3日