6.22 演習 〜 定積分
問 6.100 (定積分)
次の定積分を求めよ.
(1)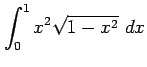 (2)
(2)
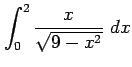 (3)
(3)
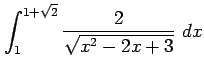 (4)
(4)
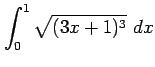
(5)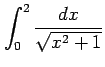 (6)
(6)
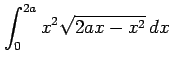 (
(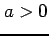 )
(7)
)
(7)
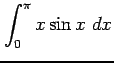 (8)
(8)
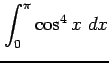
(9)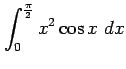 (10)
(10)
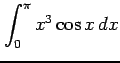 (11)
(11)
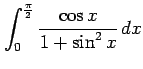 (12)
(12)
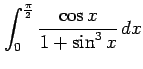
(13)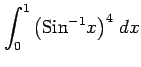 (14)
(14)
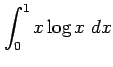 (15)
(15)
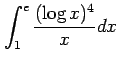 (16)
(16)
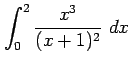
(1)
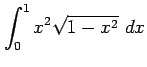 (2)
(2)
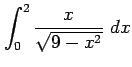 (3)
(3)
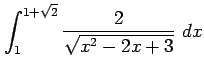 (4)
(4)
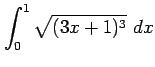
(5)
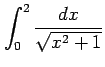 (6)
(6)
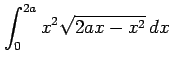 (
( (8)
(8)
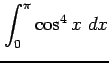
(9)
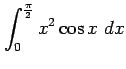 (10)
(10)
 (11)
(11)
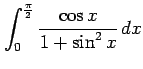 (12)
(12)
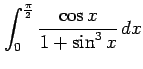
(13)
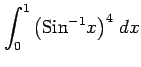 (14)
(14)
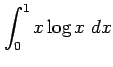 (15)
(15)
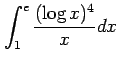 (16)
(16)
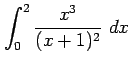
問 6.101 (定積分)
定積分
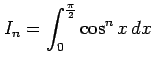
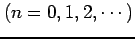 について次の問に答えよ.
について次の問に答えよ.
(1)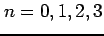 のときの
のときの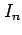 の値を求めよ.
(2)
の値を求めよ.
(2) 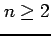 のときの
のときの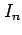 の漸化式を求めよ.
の漸化式を求めよ.
(3)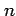 が偶数のとき
が偶数のとき
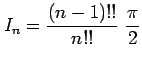 であり,
であり,
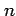 が奇数のとき
が奇数のとき
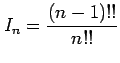 となることを示せ.
となることを示せ.
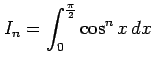
(1)
(3)
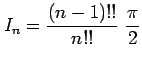 であり,
であり,
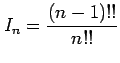 となることを示せ.
となることを示せ.
問 6.102 (曲線の長さ)
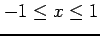 における曲線の長さを求めよ.
における曲線の長さを求めよ.
(1)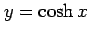 (2)
(2) 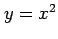
(1)
問 6.103 (面積)
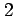 つの曲線
つの曲線
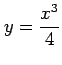 と
と 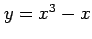 で囲まれた部分の面積を求めよ.
で囲まれた部分の面積を求めよ.
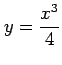 と
と
問 6.104 (面積)
楕円
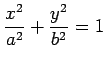
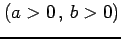 の内部の
面積を定積分を用いて求めよ.
の内部の
面積を定積分を用いて求めよ.
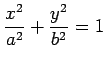
平成19年10月3日