3.16 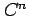 級の関数
級の関数
定理 3.44 (微分可能性と連続性)
 が
が 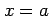 で微分可能なとき,
で微分可能なとき,
 は
は 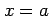 で連続である.
で連続である.
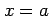 で微分が可能なので
で微分が可能なので
が成り立つ.これより
となる.ここで
とおく.このとき
である.(![[*]](crossref.png) )式を変形すると
)式を変形すると
となる.右辺を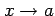 の極限をとる.
すると
の極限をとる.
すると
である.よって左辺も 0 となるので
を得る.よって は
は 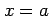 で連続である.
で連続である.
(証明) 点
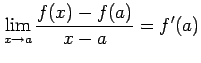 |
が成り立つ.これより
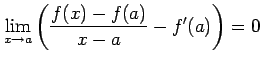 |
となる.ここで
とおく.このとき
である.(
![[*]](crossref.png) )式を変形すると
)式を変形すると
となる.右辺を
である.よって左辺も 0 となるので
を得る.よって
定義 3.45 (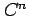 級関数)
級関数)
 が連続関数のとき
が連続関数のとき  を
を 級の関数という.
関数
級の関数という.
関数  が
が 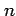 回微分可能であり,
回微分可能であり,
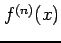 が連続関数であるとき,
が連続関数であるとき,
 を
を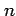 回連続微分可能な関数といい,
回連続微分可能な関数といい,
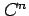 級の関数という.
また何回でも微分が可能な関数を
無限回微分可能な関数といい,
級の関数という.
また何回でも微分が可能な関数を
無限回微分可能な関数といい,
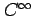 級の関数という.
級の関数という.
例 3.46 (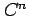 級関数の具体例)
多項式関数,
級関数の具体例)
多項式関数,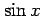 ,
, 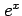 は
は 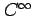 級の関数である.
級の関数である.
注意 3.47 (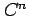 級関数の集合)
級関数の集合)
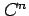 級の関数全体の集合を
級の関数全体の集合を 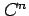 と書くとする.
このとき
と書くとする.
このとき
が成り立つ.
が成り立つ.
例 3.48 (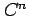 級関数の具体例)
級関数の具体例)
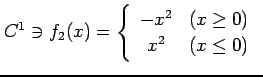 |
問 3.49 (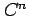 級関数)
次の関数はどの
級関数)
次の関数はどの 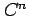 級に含まれるか述べよ.
級に含まれるか述べよ.
平成19年10月3日