2.21 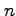 変数関数と
変数関数と 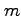 変数関数の合成関数の微分
変数関数の合成関数の微分
定理 2.88 (合成関数の微分)
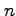 変数関数
変数関数
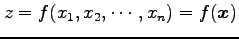 と
と
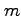 変数関数
変数関数
の合成関数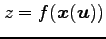 の偏微分は
の偏微分は
で与えられる.代入も含めて書くと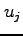 (
(
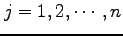 ) に関して
) に関して
と表される. また,ベクトル表記では
となる. 行列![$ \displaystyle{J=
\left[\frac{\partial x_j}{\partial u_i}\right]_{m\times n}}$](img778.png) を
ヤコビ行列(Jacobi matrix)という.
を
ヤコビ行列(Jacobi matrix)という.
 |
||
の合成関数
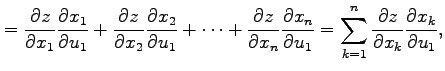 |
||
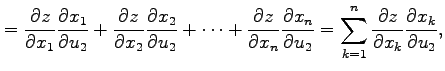 |
||
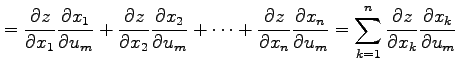 |
で与えられる.代入も含めて書くと
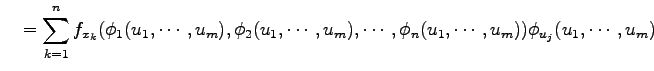 |
と表される. また,ベクトル表記では
 |
となる. 行列
![$ \displaystyle{J=
\left[\frac{\partial x_j}{\partial u_i}\right]_{m\times n}}$](img778.png) を
ヤコビ行列(Jacobi matrix)という.
を
ヤコビ行列(Jacobi matrix)という.
平成20年2月2日