2.36 1 変数の陰関数
定義 2.152 (陰関数)
変数 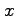 ,
, 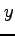 が条件
が条件 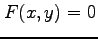 をみたすとき,
をみたすとき,
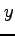 は
は 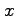 の関数
の関数 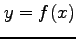 であり,
または
であり,
または 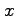 は
は 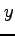 の関数
の関数 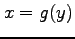 であるとみなせる.
すなわち,
であるとみなせる.
すなわち,
により定義される関数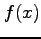 ,
,  を,
を,
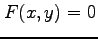 で定義される陰関数(implicit function)という.
で定義される陰関数(implicit function)という.
により定義される関数
注意 2.153 (陽関数)
関数
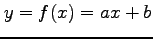 や
や
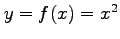 などの関数は
陽に(explicit)表されているという.
などの関数は
陽に(explicit)表されているという.
定理 2.154 (陰関数の微分)
条件 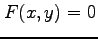 で定義される陰関数
で定義される陰関数 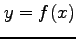 の導関数は,
の導関数は,
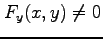 のとき
のとき
で与えられる.
である.両辺を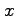 で偏微分すると
で偏微分すると
となるので,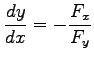 を得る.
を得る.
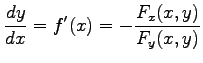 |
で与えられる.
(証明)
関数 ![]() を
を ![]() に代入すると
に代入すると
である.両辺を
| 0 | 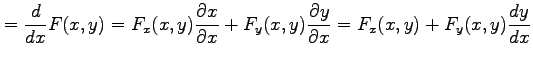 |
となるので,
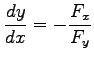 を得る.
を得る.
例 2.155 (陰関数)
条件
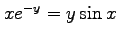 で定義される陰関数
で定義される陰関数 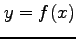 の
導関数を求める.条件
の
導関数を求める.条件
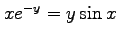 の両辺を
の両辺を 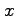 で微分すると
で微分すると
となるので,
を得る.
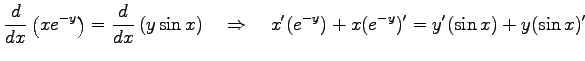 |
||
となるので,
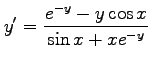 |
を得る.
例 2.156 (陰関数)
 平面内の円
平面内の円
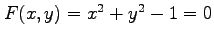 を考える.
このとき,
を考える.
このとき,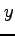 は
は 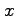 の関数
の関数 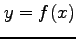 とみなされる.
これを陽に書くと
とみなされる.
これを陽に書くと
となる.これは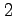 価関数である.
多価関数のままでは取り扱いに面倒が多い.
価関数である.
多価関数のままでは取り扱いに面倒が多い.
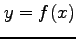 を陰関数として取り扱い導関数を求める.
条件
を陰関数として取り扱い導関数を求める.
条件 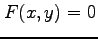 に
に 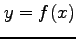 を代入すると
を代入すると
である.両辺を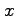 で微分すると
で微分すると
となり,
を得る. さらに微分すると 2 階導関数と 3 階導関数は
となる.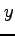 は 2 価関数であるから
は 2 価関数であるから 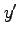 ,
, 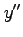 ,
, 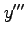 も 2 価関数である.
も 2 価関数である.
となるので,テイラー展開は
と得られる.
となる.これは
である.両辺を
となり,
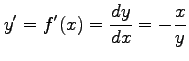 |
を得る. さらに微分すると 2 階導関数と 3 階導関数は
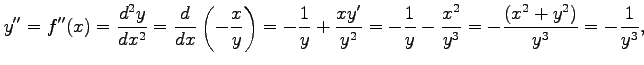 |
||
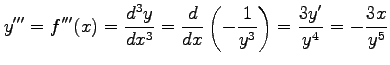 |
となる.
次に,円 ![]() 上の
点
上の
点
![]() において,
関数
において,
関数 ![]() を点
を点
![]() まわりで
テイラー展開する.
まわりで
テイラー展開する.
![]() ,
,
![]() であることに
注意すると
であることに
注意すると
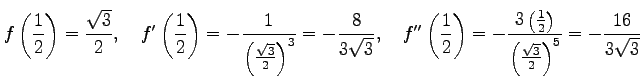 |
となるので,テイラー展開は
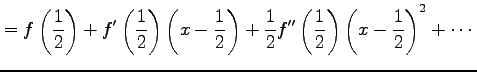 |
||
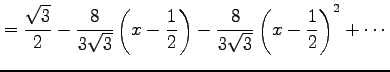 |
と得られる.
例 2.157 (陰関数)
条件
により定義される陰関数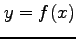 を考える.
を考える.
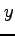 は陽に書くと,
2 次方程式
は陽に書くと,
2 次方程式
を解いて,
と表される. しかし,この形では取り扱いが面倒であるから, 陰関数として取り扱う. 導関数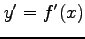 は
は
を用いて,
と求まる.
により定義される陰関数
を解いて,
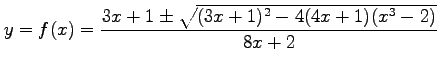 |
と表される. しかし,この形では取り扱いが面倒であるから, 陰関数として取り扱う. 導関数
を用いて,
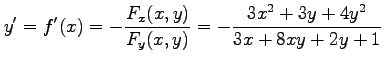 |
と求まる.
例 2.158 (陰関数)
条件
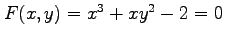 で定義される陰関数
で定義される陰関数 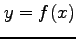 を考える.
条件
を考える.
条件
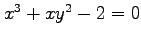 の両辺を
の両辺を 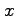 で微分すると
で微分すると
となる.よって
を得る.(☆)をさらに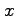 で微分すると
で微分すると
となる.両辺に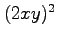 を掛けてまとめると
を掛けてまとめると
となる.また条件より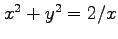 であることを用いると
であることを用いると
を得る.
であるから,
と得られる.
となる.よって
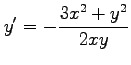 |
を得る.(☆)をさらに
| 0 | ||
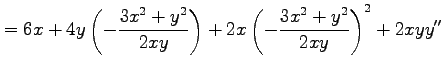 |
となる.両辺に
| 0 | ||
となる.また条件より
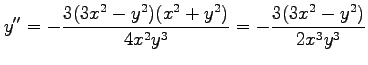 |
を得る.
曲線 ![]() 上の点
上の点 ![]() において,関数
において,関数 ![]() を
を ![]() の
まわりでテイラー展開する.
の
まわりでテイラー展開する.
![]() であることを用いて
であることを用いて
であるから,
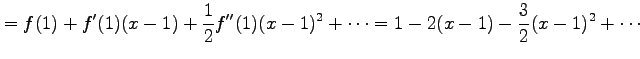 |
と得られる.
問 2.159 (陰関数)
次の条件で定義される陰関数 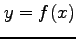 の導関数を求めよ.
の導関数を求めよ.
(1)
![]() (2)
(2)
![]() (3)
(3)
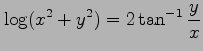
平成20年2月2日