1.24 点の直線への正射影
定義 1.124 (点の直線への正射影)
点  から直線
から直線 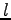 に垂線を下ろした足
に垂線を下ろした足 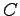 を
正射影という.
点
を
正射影という.
点  から点
から点 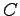 への変換を射影変換という.
への変換を射影変換という.
定理 1.125 (正射影)
点  から直線
から直線 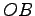 への正射影
への正射影 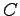 は
は
で与えられる.
となるので,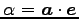 が成り立ち,
が成り立ち,
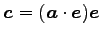 を得る.
を得る.
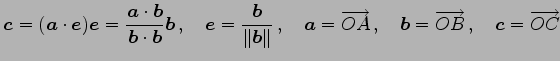 |
(133) |
で与えられる.
(証明)
直線の単位方向ベクトルを ![]() とする.
このとき
とする.
このとき
![]() とおく.
とおく.
![]() と
と ![]() が直交するので
が直交するので
![]() より
より
| 0 | (134) | |
| (135) |
となるので,
例 1.126 (正射影の具体例)
点 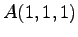 ,
,
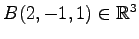 を考える.
点
を考える.
点  を直線
を直線 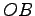 への正射影を
への正射影を 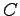 とする.
とする.
である.ベクトル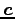 の長さは
の長さは
で与えられる. よって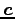 の向きは
の向きは 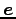 と同じなので
と同じなので
となる. 以上より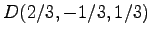 である.
である.
![]() ,
,
![]() ,
,
![]() とおく.
とおく.
![]() と向きが同じ単位ベトクルは
と向きが同じ単位ベトクルは
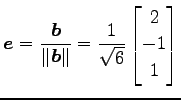 |
(136) |
である.ベクトル
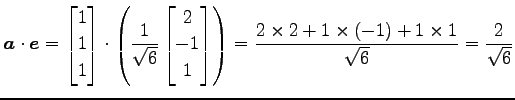 |
(137) |
で与えられる. よって
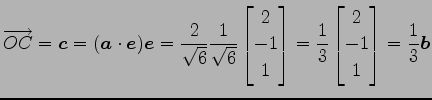 |
(138) |
となる. 以上より
例 1.127 (正射影の具体例)
点 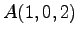 ,
, 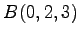 ,
,
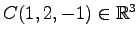 を考える.
点
を考える.
点 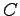 から直線
から直線 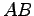 へ垂線を下ろした正射影を
へ垂線を下ろした正射影を 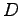 とする.
とする.
より
である.よって
となるので,
を得る.
![]() ,
,
![]() ,
,
![]() とおく.
このとき
とおく.
このとき
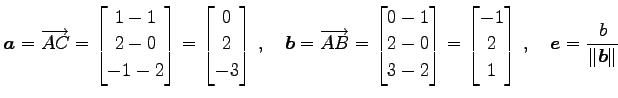 |
(139) |
より
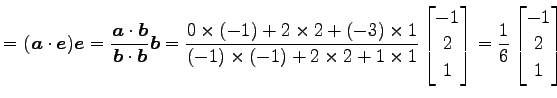 |
(140) |
である.よって
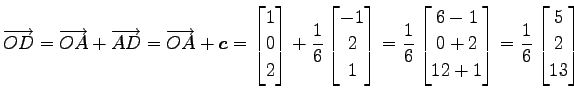 |
(141) |
となるので,
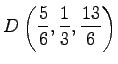 |
を得る.
定理 1.128 (点の直線への正射影)
点
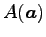 から直線
から直線
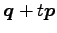 への
正射影
への
正射影
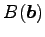 は
は
である.
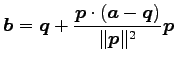 |
(142) |
である.
問 1.129 (点の直線への正射影)
これを示せ.
平成20年2月2日