1.29 平面の方程式
定義 1.149 (平面)
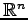 空間内の点
空間内の点 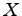 の位置ベクトルが
の位置ベクトルが
と表されるとき, 点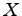 の軌跡を平面(plane)という.
の軌跡を平面(plane)という.
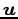 ,
, 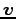 を方向ベクトル(tangent vector)という.
を方向ベクトル(tangent vector)という.
| (182) |
と表されるとき, 点
定義 1.150 (超平面)
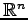 空間内の点
空間内の点 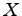 の位置ベクトルが
の位置ベクトルが
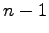 個の方向ベクトル
個の方向ベクトル
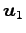 ,
, 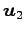 ,
,  ,
, 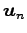 を用いて
を用いて
と表されるとき, 点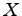 の軌跡を超平面(hyper plane)という.
の軌跡を超平面(hyper plane)という.
| (183) | ||
| (184) |
と表されるとき, 点
例 1.151 (平面の具体例)
とおく.このとき平面
を考える. 位置ベクトル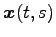 は点
は点 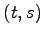 を表す.
を表す.
 ,
, 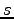 は任意の実数なので
点の軌跡は
は任意の実数なので
点の軌跡は
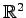 空間全体をなす.
よって
空間全体をなす.
よって
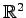 は平面である.
は平面である.
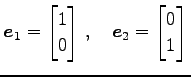 |
(185) |
とおく.このとき平面
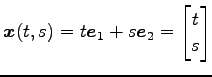 |
(186) |
を考える. 位置ベクトル
例 1.152 (
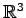 の平面の具体例)
点
の平面の具体例)
点 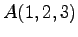 ,
, 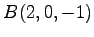 ,
,
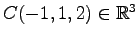 を
通る平面を考える.
点
を
通る平面を考える.
点
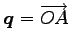 を通り
方向ベクトルが
を通り
方向ベクトルが
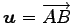 ,
,
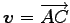 の平面と考える.
の平面と考える.
とする. 平面の方程式のパラメータ表示は
である.
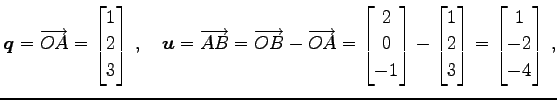 |
(187) | |
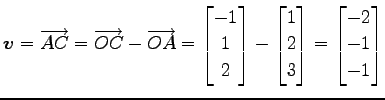 |
(188) |
とする. 平面の方程式のパラメータ表示は
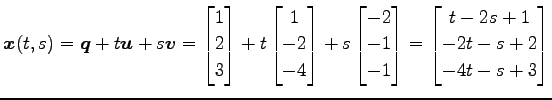 |
(189) |
である.
平成20年2月2日