1.34 点の平面への正射影
定義 1.165 (点の平面への正射影)
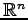 空間内の点
空間内の点  と平面を考える.
点
と平面を考える.
点  から平面へ垂線を下ろしたときの足
から平面へ垂線を下ろしたときの足 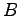 を正射影という.
点
を正射影という.
点  から点
から点 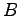 への変換を射影変換という.
への変換を射影変換という.
注意 1.166 (点の平面への正射影)
点
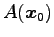 から平面
から平面
への正射影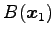 を考える.
点
を考える.
点  から平面への垂線は平面と直交する.
よって垂線の方向ベクトルと平面の法線ベクトル
から平面への垂線は平面と直交する.
よって垂線の方向ベクトルと平面の法線ベクトル 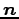 は等しい.
垂線は点
は等しい.
垂線は点
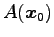 を通り
方向ベクトルが
を通り
方向ベクトルが 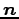 であるので,
垂線の方程式は
であるので,
垂線の方程式は
と表される. 垂線と平面の交点が正射影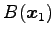 である.
交点
である.
交点
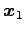 を求める.
垂線の方程式を平面の方程式に代入すると
を求める.
垂線の方程式を平面の方程式に代入すると
であり, についてまとめると
についてまとめると
が成り立つ. これを垂線の方程式に代入し,交点
を得る.
| (224) |
への正射影
| (225) |
と表される. 垂線と平面の交点が正射影
| (226) |
であり,
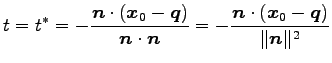 |
(227) |
が成り立つ. これを垂線の方程式に代入し,交点
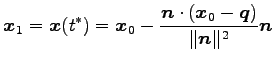 |
(228) |
を得る.
例 1.167 (点の平面への正射影)
点 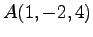 の平面
の平面
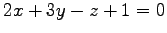 への正射影
への正射影 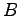 を考える.
平面の法線ベクトルは
を考える.
平面の法線ベクトルは
![$ \vec{n}=\begin{bmatrix}{2}\\ [-.5ex]{3}\\ [-.5ex]{-1}\end{bmatrix}$](img885.png) であるから,
点
であるから,
点  を通り平面に垂直な直線の方程式は
を通り平面に垂直な直線の方程式は
となる. パラメータ表示すると
である. これを平面の方程式に代入すると
より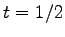 を得る.
これを垂線の方程式に代入すると
を得る.
これを垂線の方程式に代入すると
であり,正射影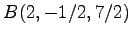 を得る.
を得る.
![$ \vec{n}=\begin{bmatrix}{2}\\ [-.5ex]{3}\\ [-.5ex]{-1}\end{bmatrix}$](img885.png) であるから,
点
であるから,
点 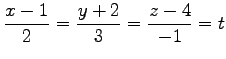 |
(229) |
となる. パラメータ表示すると
| (230) |
である. これを平面の方程式に代入すると
| (231) |
より
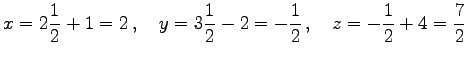 |
(232) |
であり,正射影
平成20年2月2日