2.18 行列のベクトルへの分割
例 2.73 (行列を列ベクトル,行ベクトルへ分割)
行列を分割し列ベクトルと行ベクトルでそれぞれ表す.
行列
を考える. 行列を一列ずつ縦に分割し,
と表わす. ただし,
とおく. 行列を一行ずつ分割し,
と表わす. ただし,
とおく.
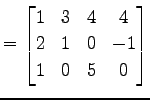 |
(362) |
を考える. 行列を一列ずつ縦に分割し,
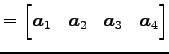 |
(363) |
と表わす. ただし,
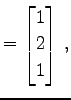 |
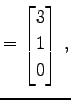 |
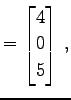 |
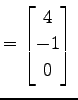 |
: |
(364) |
とおく. 行列を一行ずつ分割し,
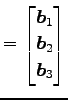 |
(365) |
と表わす. ただし,
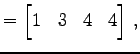 |
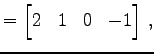 |
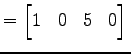 |
(366) | |||
| : |
とおく.
問 2.74
教科書(p.14)問題1.3.
例 2.75 (行列をベクトルに分割したときの積の表現)
行列の積をベクトルを用いて表現する.
行列  と行列
と行列 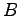 の積
の積 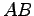 を考える.
行列
を考える.
行列  は
は
のように行ベクトルに分割する. 行列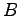 は
は
のように列ベクトルに分割する. このとき積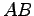 は
は
と表わされる. ここで
となることに注意する.
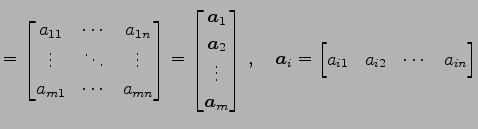 :行ベクトル :行ベクトル |
(367) |
のように行ベクトルに分割する. 行列
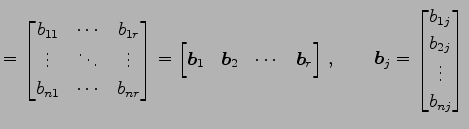 :列ベクトル :列ベクトル |
(368) |
のように列ベクトルに分割する. このとき積
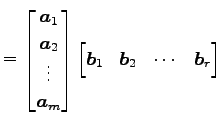 |
(369) | |
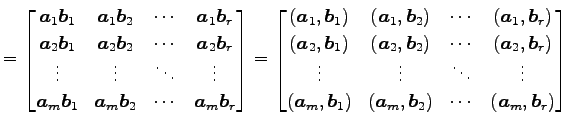 |
(370) | |
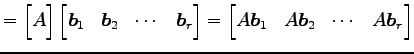 |
(371) | |
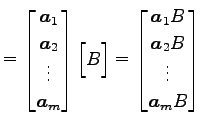 |
(372) |
と表わされる. ここで
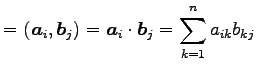 |
(373) |
となることに注意する.
例 2.76 (行列の積の具体例)
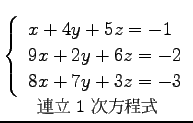 |
(374) | |
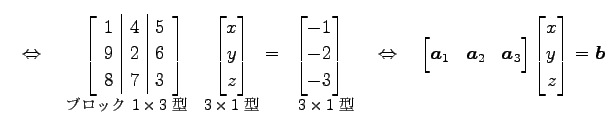 |
(375) | |
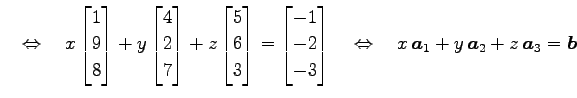 |
(376) |
平成20年2月2日