4.13 演習問題 〜 行列式,行列式の性質
問 4.80 (置換)
次の置換の積を計算せよ.
(1)![$ \begin{pmatrix}
1\! & \!2\! & \!3 \\ [-0.5ex] 3\! & \!1\! & \!2
\end{pmatrix}\begin{pmatrix}
1\! & \!2\! & \!3 \\ [-0.5ex] 3\! & \!1\! & \!2
\end{pmatrix}$](img2175.png) (2)
(2)
![$ \begin{pmatrix}
1\! & \!2\! & \!3\! & \!4 \\ [-0.5ex] 3\! & \!4\! & \!2\! & \!...
...}
1\! & \!2\! & \!3\! & \!4 \\ [-0.5ex] 4\! & \!3\! & \!2\! & \!1
\end{pmatrix}$](img2176.png) (3)
(3)
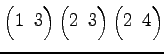
(4)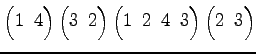
(1)
![$ \begin{pmatrix}
1\! & \!2\! & \!3 \\ [-0.5ex] 3\! & \!1\! & \!2
\end{pmatrix}\begin{pmatrix}
1\! & \!2\! & \!3 \\ [-0.5ex] 3\! & \!1\! & \!2
\end{pmatrix}$](img2175.png) (2)
(2)
![$ \begin{pmatrix}
1\! & \!2\! & \!3\! & \!4 \\ [-0.5ex] 3\! & \!4\! & \!2\! & \!...
...}
1\! & \!2\! & \!3\! & \!4 \\ [-0.5ex] 4\! & \!3\! & \!2\! & \!1
\end{pmatrix}$](img2176.png) (3)
(3)
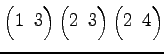
(4)
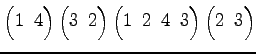
問 4.81 (置換)
次の置換を互換の積に分解せよ.また各々の置換の符号
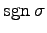 を求めよ.
を求めよ.
(1)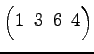 (2)
(2)
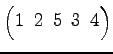 (3)
(3)
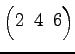 (4)
(4)
![$ \begin{pmatrix}
1\! & \!2\! & \!3\! & \!4\! & \!5\! & \!6\! & \!7 \\ [-0.5ex] 3\! & \!7\! & \!4\! & \!1\! & \!2\!
& \!5\! & \!6
\end{pmatrix}$](img2183.png)
(5)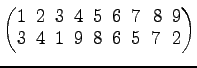 (6)
(6)
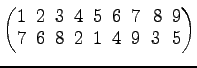
(1)
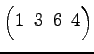 (2)
(2)
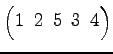 (3)
(3)
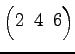 (4)
(4)
![$ \begin{pmatrix}
1\! & \!2\! & \!3\! & \!4\! & \!5\! & \!6\! & \!7 \\ [-0.5ex] 3\! & \!7\! & \!4\! & \!1\! & \!2\!
& \!5\! & \!6
\end{pmatrix}$](img2183.png)
(5)
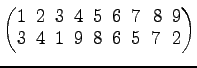 (6)
(6)
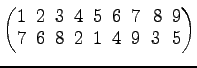
問 4.82 (置換)
置換
![$ \sigma=\begin{pmatrix}
1\! & \!2\! & \!3\! & \!4\! & \!5\! & \!6\! & \!7 \\ [-0.5ex]
4\! & \!1\! & \!6\! & \!2\! & \!7\! & \!5\! & \!3
\end{pmatrix}$](img2186.png) を巡回置換の積で表せ.
を巡回置換の積で表せ.
![$ \sigma=\begin{pmatrix}
1\! & \!2\! & \!3\! & \!4\! & \!5\! & \!6\! & \!7 \\ [-0.5ex]
4\! & \!1\! & \!6\! & \!2\! & \!7\! & \!5\! & \!3
\end{pmatrix}$](img2186.png) を巡回置換の積で表せ.
を巡回置換の積で表せ.
問 4.83 (行列式)
次の行列式の値を求めよ.
(1)![$ \begin{vmatrix}
1\! & \!3 \\ [-0.5ex] 2\! & \!4
\end{vmatrix}$](img2187.png) (2)
(2)
![$ \begin{vmatrix}
1\! & \!2 \\ [-0.5ex] 4\! & \!-1
\end{vmatrix}$](img2188.png) (3)
(3)
![$ \begin{vmatrix}
3\! & \!-1 \\ [-0.5ex] 4\! & \!2
\end{vmatrix}$](img2189.png) (4)
(4)
![$ \begin{vmatrix}
-2\! & \!5 \\ [-0.5ex] 3\! & \!4
\end{vmatrix}$](img2190.png) (5)
(5)
![$ \begin{vmatrix}
-1\! & \!3 \\ [-0.5ex] -2\! & \!-1
\end{vmatrix}$](img2191.png) (6)
(6)
![$ \begin{vmatrix}
1\! & \!2\! & \!3 \\ [-0.5ex] 0\! & \!5\! & \!2 \\ [-0.5ex] 7\! &
1\! & \!6
\end{vmatrix}$](img2192.png) (7)
(7)
![$ \begin{vmatrix}
1\! & \!0\! & \!2 \\ [-0.5ex] 3\! & \!0\! & \!4 \\ [-0.5ex] 2\! &
-5\! & \!1
\end{vmatrix}$](img2193.png)
(8)![$ \begin{vmatrix}
3\! & \!-2\! & \!5 \\ [-0.5ex] -4\! & \!3\! & \!-6 \\ [-0.5ex] 5\! &
-3\! & \!9
\end{vmatrix}$](img2194.png) (9)
(9)
![$ \begin{vmatrix}
3\! & \!4\! & \!5 \\ [-0.5ex] 1\! & \!2\! & \!3 \\ [-0.5ex] -2\! &
5\! & \!-4
\end{vmatrix}$](img2195.png) (10)
(10)
![$ \begin{vmatrix}
0\! & \!0\! & \!4 \\ [-0.5ex] 0\! & \!-5\! & \!7 \\ [-0.5ex] 3\! &
2\! & \!1
\end{vmatrix}$](img2196.png) (11)
(11)
![$ \begin{vmatrix}
2\! & \!3\! & \!5 \\ [-0.5ex] 8\! & \!13\! & \!-1 \\ [-0.5ex] 6\! &
-9\! & \!6
\end{vmatrix}$](img2197.png) (12)
(12)
![$ \begin{vmatrix}
1\! & \!2\! & \!1 \\ [-0.5ex] 2\! & \!-1\! & \!1 \\ [-0.5ex] 3\! &
1\! & \!2
\end{vmatrix}$](img2198.png)
(13)![$ \begin{vmatrix}
1\! & \!2\! & \!-2 \\ [-0.5ex] 1\! & \!5\! & \!-3 \\ [-0.5ex] 2\! &
7\! & \!-5
\end{vmatrix}$](img2199.png) (14)
(14)
![$ \begin{vmatrix}
1\! & \!2\! & \!3 \\ [-0.5ex] 4\! & \!-2\! & \!3 \\ [-0.5ex] 2\! &
5\! & \!-1
\end{vmatrix}$](img2200.png) (15)
(15)
![$ \begin{vmatrix}
3\! & \!2\! & \!-4 \\ [-0.5ex] 1\! & \!0\! & \!-2 \\ [-0.5ex] -2\! &
3\! & \!3
\end{vmatrix}$](img2201.png) (16)
(16)
![$ \begin{vmatrix}
2\! & \!1\! & \!-1 \\ [-0.5ex] 1\! & \!3\! & \!1 \\ [-0.5ex] 2\! &
-1\! & \!1
\end{vmatrix}$](img2202.png) (17)
(17)
![$ \begin{vmatrix}
1\! & \!3\! & \!3 \\ [-0.5ex] 2\! & \!-1\! & \!-1 \\ [-0.5ex] 4\! &
3\! & \!3
\end{vmatrix}$](img2203.png)
(18)![$ \begin{vmatrix}
7\! & \!3\! & \!-5 \\ [-0.5ex] 3\! & \!-2\! & \!6 \\ [-0.5ex] 5\! &
5\! & \!3
\end{vmatrix}$](img2204.png) (19)
(19)
![$ \begin{vmatrix}
3\! & \!-1\! & \!5 \\ [-0.5ex] 3\! & \!4\! & \!-1 \\ [-0.5ex] -2\! &
-1\! & \!-2
\end{vmatrix}$](img2205.png) (20)
(20)
![$ \begin{vmatrix}
1\! & \!-4\! & \!1 \\ [-0.5ex] 3\! & \!-6\! & \!7 \\ [-0.5ex] 2\! &
-1\! & \!-3
\end{vmatrix}$](img2206.png) (21)
(21)
![$ \begin{vmatrix}
2\! & \!1\! & \!1 \\ [-0.5ex] -4\! & \!5\! & \!3 \\ [-0.5ex] -5\! &
4\! & \!2
\end{vmatrix}$](img2207.png) (22)
(22)
![$ \begin{vmatrix}
5\! & \!-3\! & \!14 \\ [-0.5ex] -5\! & \!6\! & \!7 \\ [-0.5ex] 10\! &
3\! & \!-7
\end{vmatrix}$](img2208.png)
(23)![$ \begin{vmatrix}
2\! & \!16\! & \!3 \\ [-0.5ex] 4\! & \!8\! & \!-6 \\ [-0.5ex] 8\! &
8\! & \!12
\end{vmatrix}$](img2209.png) (24)
(24)
![$ \begin{vmatrix}
25\! & \!-15\! & \!10 \\ [-0.5ex] -10\! & \!6\! & \!4 \\ [-0.5ex] 1\! &
9\! & \!0
\end{vmatrix}$](img2210.png) (25)
(25)
![$ \begin{vmatrix}
10\! & \!19\! & \!16 \\ [-0.5ex] 6\! & \!11\! & \!13 \\ [-0.5ex] 5\! &
13\! & \!12
\end{vmatrix}$](img2211.png) (26)
(26)
![$ \begin{vmatrix}
20\! & \!19\! & \!16 \\ [-0.5ex] 12\! & \!11\! & \!13 \\ [-0.5ex] 10\! &
13\! & \!12
\end{vmatrix}$](img2212.png) (27)
(27)
![$ \begin{vmatrix}
12\! & \!16\! & \!32 \\ [-0.5ex] -6\! & \!13\! & \!4 \\ [-0.5ex] 15\! &
10\! & \!-20
\end{vmatrix}$](img2213.png)
(28)![$ \begin{vmatrix}
1/4\! & \!1/6\! & \!2/3 \\ [-0.5ex] 1/12\! & \!1/6\! & \!1/4 \\ [-0.5ex] 1/4\! &
0\! & \!1/6
\end{vmatrix}$](img2214.png) (29)
(29)
![$ \begin{vmatrix}
99\! & \!100\! & \!101 \\ [-0.5ex] 100\! & \!99\! & \!100 \\ [-0.5ex] 101\! &
101\! & \!99
\end{vmatrix}$](img2215.png) (30)
(30)
![$ \begin{vmatrix}
2\! & \!-4\! & \!-5\! & \!3 \\ [-0.5ex] -6\! & \!13\! & \!14\!...
...1\! &
-2\! & \!-2\! & \!-8 \\ [-0.5ex] 2\! & \!-5\! & \!0\! & \!5
\end{vmatrix}$](img2216.png) (31)
(31)
![$ \begin{vmatrix}
2\! & \!0\! & \!1\! & \!-2 \\ [-0.5ex] 1\! & \!3\! & \!2\! & \...
...] -1\! &
5\! & \!1\! & \!1 \\ [-0.5ex] 2\! & \!7\! & \!-6\! & \!3
\end{vmatrix}$](img2217.png)
(32)![$ \begin{vmatrix}
1\! & \!0\! & \!5\! & \!0 \\ [-0.5ex] 0\! & \!3\! & \!0\! & \!...
...ex] 4\! &
0\! & \!2\! & \!0 \\ [-0.5ex] 0\! & \!3\! & \!0\! & \!7
\end{vmatrix}$](img2218.png) (33)
(33)
![$ \begin{vmatrix}
3\! & \!-3\! & \!-4\! & \!4 \\ [-0.5ex] 1\! & \!0\! & \!3\! & ...
...x] 4\! &
1\! & \!2\! & \!7 \\ [-0.5ex] -1\! & \!2\! & \!2\! & \!0
\end{vmatrix}$](img2219.png) (34)
(34)
![$ \begin{vmatrix}
5\! & \!4\! & \!7\! & \!9 \\ [-0.5ex] -1\! & \!3\! & \!9\! & \...
... 1\! &
-3\! & \!-8\! & \!1 \\ [-0.5ex] 5\! & \!4\! & \!2\! & \!11
\end{vmatrix}$](img2220.png) (35)
(35)
![$ \begin{vmatrix}
1\! & \!-1\! & \!2\! & \!1 \\ [-0.5ex] 2\! & \!-1\! & \!1\! & ...
...x] -1\! &
1\! & \!2\! & \!1 \\ [-0.5ex] 2\! & \!1\! & \!1\! & \!1
\end{vmatrix}$](img2221.png)
(36)![$ \begin{vmatrix}
3\! & \!1\! & \!3\! & \!5 \\ [-0.5ex] 6\! & \!2\! & \!2\! & \!...
...x] -3\! &
1\! & \!0\! & \!1 \\ [-0.5ex] 3\! & \!1\! & \!1\! & \!6
\end{vmatrix}$](img2222.png) (37)
(37)
![$ \begin{vmatrix}
2\! & \!-2\! & \!4\! & \!2 \\ [-0.5ex] 2\! & \!-1\! & \!6\! & ...
...\! &
-2\! & \!12\! & \!12 \\ [-0.5ex] -1\! & \!3\! & \!-4\! & \!4
\end{vmatrix}$](img2223.png) (38)
(38)
![$ \begin{vmatrix}
2\! & \!-1\! & \!2\! & \!1 \\ [-0.5ex] 4\! & \!-1\! & \!6\! & ...
...] -2\! &
2\! & \!4\! & \!2 \\ [-0.5ex] -6\! & \!5\! & \!3\! & \!9
\end{vmatrix}$](img2224.png) (39)
(39)
![$ \begin{vmatrix}
-1\! & \!-4\! & \!3\! & \!4 \\ [-0.5ex] 1\! & \!2\! & \!-3\! &...
...] 7\! &
9\! & \!4\! & \!2 \\ [-0.5ex] -9\! & \!7\! & \!-3\! & \!6
\end{vmatrix}$](img2225.png)
(40)![$ \begin{vmatrix}
0\! & \!-3\! & \!-6\! & \!15 \\ [-0.5ex] -2\! & \!5\! & \!14\!...
...! &
-3\! & \!-2\! & \!5 \\ [-0.5ex] 15\! & \!10\! & \!10\! & \!-5
\end{vmatrix}$](img2226.png) (41)
(41)
![$ \begin{vmatrix}
0\! & \!0\! & \!0\! & \!0\! & \!3 \\ [-0.5ex] 0\! & \!2\! & \!...
... \!1\! & \!2\! & \!2 \\ [-0.5ex] 8\! &
1\! & \!2\! & \!3\! & \!4
\end{vmatrix}$](img2227.png) (42)
(42)
![$ \begin{vmatrix}
1\! & \!-1\! & \!-1\! & \!1\! & \!-1 \\ [-0.5ex] 1\! & \!-1\! ...
...!1\! & \!1\! & \!1 \\ [-0.5ex] 1\! &
1\! & \!1\! & \!-1\! & \!-1
\end{vmatrix}$](img2228.png)
(43)![$ \begin{vmatrix}
1\! & \!0\! & \!0\! & \!1\! & \!1 \\ [-0.5ex] 0\! & \!1\! & \!...
...\!3\! & \!1\! & \!0 \\ [-0.5ex] 1\! &
1\! & \!-2\! & \!0\! & \!0
\end{vmatrix}$](img2229.png) (44)
(44)
![$ \begin{vmatrix}
3\! & \!5\! & \!1\! & \!2\! & \!-1 \\ [-0.5ex] 2\! & \!6\! & \...
...\!3\! & \!2\! & \!5 \\ [-0.5ex] 0\! &
0\! & \!0\! & \!0\! & \!-6
\end{vmatrix}$](img2230.png) (45)
(45)
![$ \begin{vmatrix}
3\! & \!5\! & \!1\! & \!2\! & \!1 \\ [-0.5ex] 2\! & \!6\! & \!...
... \!0\! & \!0\! & \!0 \\ [-0.5ex] 1\! &
5\! & \!0\! & \!0\! & \!0
\end{vmatrix}$](img2231.png)
(1)
![$ \begin{vmatrix}
1\! & \!2 \\ [-0.5ex] 4\! & \!-1
\end{vmatrix}$](img2188.png) (3)
(3)
![$ \begin{vmatrix}
3\! & \!-1 \\ [-0.5ex] 4\! & \!2
\end{vmatrix}$](img2189.png) (4)
(4)
![$ \begin{vmatrix}
-2\! & \!5 \\ [-0.5ex] 3\! & \!4
\end{vmatrix}$](img2190.png) (5)
(5)
![$ \begin{vmatrix}
-1\! & \!3 \\ [-0.5ex] -2\! & \!-1
\end{vmatrix}$](img2191.png) (6)
(6)
![$ \begin{vmatrix}
1\! & \!2\! & \!3 \\ [-0.5ex] 0\! & \!5\! & \!2 \\ [-0.5ex] 7\! &
1\! & \!6
\end{vmatrix}$](img2192.png) (7)
(7)
![$ \begin{vmatrix}
1\! & \!0\! & \!2 \\ [-0.5ex] 3\! & \!0\! & \!4 \\ [-0.5ex] 2\! &
-5\! & \!1
\end{vmatrix}$](img2193.png)
(8)
![$ \begin{vmatrix}
3\! & \!-2\! & \!5 \\ [-0.5ex] -4\! & \!3\! & \!-6 \\ [-0.5ex] 5\! &
-3\! & \!9
\end{vmatrix}$](img2194.png) (9)
(9)
![$ \begin{vmatrix}
3\! & \!4\! & \!5 \\ [-0.5ex] 1\! & \!2\! & \!3 \\ [-0.5ex] -2\! &
5\! & \!-4
\end{vmatrix}$](img2195.png) (10)
(10)
![$ \begin{vmatrix}
0\! & \!0\! & \!4 \\ [-0.5ex] 0\! & \!-5\! & \!7 \\ [-0.5ex] 3\! &
2\! & \!1
\end{vmatrix}$](img2196.png) (11)
(11)
![$ \begin{vmatrix}
2\! & \!3\! & \!5 \\ [-0.5ex] 8\! & \!13\! & \!-1 \\ [-0.5ex] 6\! &
-9\! & \!6
\end{vmatrix}$](img2197.png) (12)
(12)
![$ \begin{vmatrix}
1\! & \!2\! & \!1 \\ [-0.5ex] 2\! & \!-1\! & \!1 \\ [-0.5ex] 3\! &
1\! & \!2
\end{vmatrix}$](img2198.png)
(13)
![$ \begin{vmatrix}
1\! & \!2\! & \!-2 \\ [-0.5ex] 1\! & \!5\! & \!-3 \\ [-0.5ex] 2\! &
7\! & \!-5
\end{vmatrix}$](img2199.png) (14)
(14)
![$ \begin{vmatrix}
1\! & \!2\! & \!3 \\ [-0.5ex] 4\! & \!-2\! & \!3 \\ [-0.5ex] 2\! &
5\! & \!-1
\end{vmatrix}$](img2200.png) (15)
(15)
![$ \begin{vmatrix}
3\! & \!2\! & \!-4 \\ [-0.5ex] 1\! & \!0\! & \!-2 \\ [-0.5ex] -2\! &
3\! & \!3
\end{vmatrix}$](img2201.png) (16)
(16)
![$ \begin{vmatrix}
2\! & \!1\! & \!-1 \\ [-0.5ex] 1\! & \!3\! & \!1 \\ [-0.5ex] 2\! &
-1\! & \!1
\end{vmatrix}$](img2202.png) (17)
(17)
![$ \begin{vmatrix}
1\! & \!3\! & \!3 \\ [-0.5ex] 2\! & \!-1\! & \!-1 \\ [-0.5ex] 4\! &
3\! & \!3
\end{vmatrix}$](img2203.png)
(18)
![$ \begin{vmatrix}
7\! & \!3\! & \!-5 \\ [-0.5ex] 3\! & \!-2\! & \!6 \\ [-0.5ex] 5\! &
5\! & \!3
\end{vmatrix}$](img2204.png) (19)
(19)
![$ \begin{vmatrix}
3\! & \!-1\! & \!5 \\ [-0.5ex] 3\! & \!4\! & \!-1 \\ [-0.5ex] -2\! &
-1\! & \!-2
\end{vmatrix}$](img2205.png) (20)
(20)
![$ \begin{vmatrix}
1\! & \!-4\! & \!1 \\ [-0.5ex] 3\! & \!-6\! & \!7 \\ [-0.5ex] 2\! &
-1\! & \!-3
\end{vmatrix}$](img2206.png) (21)
(21)
![$ \begin{vmatrix}
2\! & \!1\! & \!1 \\ [-0.5ex] -4\! & \!5\! & \!3 \\ [-0.5ex] -5\! &
4\! & \!2
\end{vmatrix}$](img2207.png) (22)
(22)
![$ \begin{vmatrix}
5\! & \!-3\! & \!14 \\ [-0.5ex] -5\! & \!6\! & \!7 \\ [-0.5ex] 10\! &
3\! & \!-7
\end{vmatrix}$](img2208.png)
(23)
![$ \begin{vmatrix}
2\! & \!16\! & \!3 \\ [-0.5ex] 4\! & \!8\! & \!-6 \\ [-0.5ex] 8\! &
8\! & \!12
\end{vmatrix}$](img2209.png) (24)
(24)
![$ \begin{vmatrix}
25\! & \!-15\! & \!10 \\ [-0.5ex] -10\! & \!6\! & \!4 \\ [-0.5ex] 1\! &
9\! & \!0
\end{vmatrix}$](img2210.png) (25)
(25)
![$ \begin{vmatrix}
10\! & \!19\! & \!16 \\ [-0.5ex] 6\! & \!11\! & \!13 \\ [-0.5ex] 5\! &
13\! & \!12
\end{vmatrix}$](img2211.png) (26)
(26)
![$ \begin{vmatrix}
20\! & \!19\! & \!16 \\ [-0.5ex] 12\! & \!11\! & \!13 \\ [-0.5ex] 10\! &
13\! & \!12
\end{vmatrix}$](img2212.png) (27)
(27)
![$ \begin{vmatrix}
12\! & \!16\! & \!32 \\ [-0.5ex] -6\! & \!13\! & \!4 \\ [-0.5ex] 15\! &
10\! & \!-20
\end{vmatrix}$](img2213.png)
(28)
![$ \begin{vmatrix}
1/4\! & \!1/6\! & \!2/3 \\ [-0.5ex] 1/12\! & \!1/6\! & \!1/4 \\ [-0.5ex] 1/4\! &
0\! & \!1/6
\end{vmatrix}$](img2214.png) (29)
(29)
![$ \begin{vmatrix}
99\! & \!100\! & \!101 \\ [-0.5ex] 100\! & \!99\! & \!100 \\ [-0.5ex] 101\! &
101\! & \!99
\end{vmatrix}$](img2215.png) (30)
(30)
![$ \begin{vmatrix}
2\! & \!-4\! & \!-5\! & \!3 \\ [-0.5ex] -6\! & \!13\! & \!14\!...
...1\! &
-2\! & \!-2\! & \!-8 \\ [-0.5ex] 2\! & \!-5\! & \!0\! & \!5
\end{vmatrix}$](img2216.png) (31)
(31)
![$ \begin{vmatrix}
2\! & \!0\! & \!1\! & \!-2 \\ [-0.5ex] 1\! & \!3\! & \!2\! & \...
...] -1\! &
5\! & \!1\! & \!1 \\ [-0.5ex] 2\! & \!7\! & \!-6\! & \!3
\end{vmatrix}$](img2217.png)
(32)
![$ \begin{vmatrix}
1\! & \!0\! & \!5\! & \!0 \\ [-0.5ex] 0\! & \!3\! & \!0\! & \!...
...ex] 4\! &
0\! & \!2\! & \!0 \\ [-0.5ex] 0\! & \!3\! & \!0\! & \!7
\end{vmatrix}$](img2218.png) (33)
(33)
![$ \begin{vmatrix}
3\! & \!-3\! & \!-4\! & \!4 \\ [-0.5ex] 1\! & \!0\! & \!3\! & ...
...x] 4\! &
1\! & \!2\! & \!7 \\ [-0.5ex] -1\! & \!2\! & \!2\! & \!0
\end{vmatrix}$](img2219.png) (34)
(34)
![$ \begin{vmatrix}
5\! & \!4\! & \!7\! & \!9 \\ [-0.5ex] -1\! & \!3\! & \!9\! & \...
... 1\! &
-3\! & \!-8\! & \!1 \\ [-0.5ex] 5\! & \!4\! & \!2\! & \!11
\end{vmatrix}$](img2220.png) (35)
(35)
![$ \begin{vmatrix}
1\! & \!-1\! & \!2\! & \!1 \\ [-0.5ex] 2\! & \!-1\! & \!1\! & ...
...x] -1\! &
1\! & \!2\! & \!1 \\ [-0.5ex] 2\! & \!1\! & \!1\! & \!1
\end{vmatrix}$](img2221.png)
(36)
![$ \begin{vmatrix}
3\! & \!1\! & \!3\! & \!5 \\ [-0.5ex] 6\! & \!2\! & \!2\! & \!...
...x] -3\! &
1\! & \!0\! & \!1 \\ [-0.5ex] 3\! & \!1\! & \!1\! & \!6
\end{vmatrix}$](img2222.png) (37)
(37)
![$ \begin{vmatrix}
2\! & \!-2\! & \!4\! & \!2 \\ [-0.5ex] 2\! & \!-1\! & \!6\! & ...
...\! &
-2\! & \!12\! & \!12 \\ [-0.5ex] -1\! & \!3\! & \!-4\! & \!4
\end{vmatrix}$](img2223.png) (38)
(38)
![$ \begin{vmatrix}
2\! & \!-1\! & \!2\! & \!1 \\ [-0.5ex] 4\! & \!-1\! & \!6\! & ...
...] -2\! &
2\! & \!4\! & \!2 \\ [-0.5ex] -6\! & \!5\! & \!3\! & \!9
\end{vmatrix}$](img2224.png) (39)
(39)
![$ \begin{vmatrix}
-1\! & \!-4\! & \!3\! & \!4 \\ [-0.5ex] 1\! & \!2\! & \!-3\! &...
...] 7\! &
9\! & \!4\! & \!2 \\ [-0.5ex] -9\! & \!7\! & \!-3\! & \!6
\end{vmatrix}$](img2225.png)
(40)
![$ \begin{vmatrix}
0\! & \!-3\! & \!-6\! & \!15 \\ [-0.5ex] -2\! & \!5\! & \!14\!...
...! &
-3\! & \!-2\! & \!5 \\ [-0.5ex] 15\! & \!10\! & \!10\! & \!-5
\end{vmatrix}$](img2226.png) (41)
(41)
![$ \begin{vmatrix}
0\! & \!0\! & \!0\! & \!0\! & \!3 \\ [-0.5ex] 0\! & \!2\! & \!...
... \!1\! & \!2\! & \!2 \\ [-0.5ex] 8\! &
1\! & \!2\! & \!3\! & \!4
\end{vmatrix}$](img2227.png) (42)
(42)
![$ \begin{vmatrix}
1\! & \!-1\! & \!-1\! & \!1\! & \!-1 \\ [-0.5ex] 1\! & \!-1\! ...
...!1\! & \!1\! & \!1 \\ [-0.5ex] 1\! &
1\! & \!1\! & \!-1\! & \!-1
\end{vmatrix}$](img2228.png)
(43)
![$ \begin{vmatrix}
1\! & \!0\! & \!0\! & \!1\! & \!1 \\ [-0.5ex] 0\! & \!1\! & \!...
...\!3\! & \!1\! & \!0 \\ [-0.5ex] 1\! &
1\! & \!-2\! & \!0\! & \!0
\end{vmatrix}$](img2229.png) (44)
(44)
![$ \begin{vmatrix}
3\! & \!5\! & \!1\! & \!2\! & \!-1 \\ [-0.5ex] 2\! & \!6\! & \...
...\!3\! & \!2\! & \!5 \\ [-0.5ex] 0\! &
0\! & \!0\! & \!0\! & \!-6
\end{vmatrix}$](img2230.png) (45)
(45)
![$ \begin{vmatrix}
3\! & \!5\! & \!1\! & \!2\! & \!1 \\ [-0.5ex] 2\! & \!6\! & \!...
... \!0\! & \!0\! & \!0 \\ [-0.5ex] 1\! &
5\! & \!0\! & \!0\! & \!0
\end{vmatrix}$](img2231.png)
問 4.84 (行列式)
次の行列式を計算せよ.
(1)![$ \begin{vmatrix}
1\! & \!1\! & \!1 \\ [-0.5ex] a\! & \!b\! & \!c \\ [-0.5ex] a^2\! &
b^2\! & \!c^2
\end{vmatrix}$](img2232.png) (2)
(2)
![$ \begin{vmatrix}
a\! & \!b\! & \!c \\ [-0.5ex] a^2\! & \!b^2\! & \!c^2 \\ [-0.5ex] b+c\! &
c+a\! & \!a+b
\end{vmatrix}$](img2233.png) (3)
(3)
![$ \begin{vmatrix}
a\! & \!b\! & \!b\! & \!b \\ [-0.5ex] a\! & \!b\! & \!a\! & \!...
...ex] a\! &
a\! & \!b\! & \!a \\ [-0.5ex] b\! & \!b\! & \!b\! & \!a
\end{vmatrix}$](img2234.png) (4)
(4)
![$ \begin{vmatrix}
0\! & \!a\! & \!b\! & \!c \\ [-0.5ex] a\! & \!0\! & \!c\! & \!...
...ex] b\! &
c\! & \!0\! & \!a \\ [-0.5ex] c\! & \!b\! & \!a\! & \!0
\end{vmatrix}$](img2235.png) (5)
(5)
![$ \begin{vmatrix}
1\! & \!a\! & \!d\! & \!b+c \\ [-0.5ex] 1\! & \!b\! & \!a\! & ...
...1\! &
c\! & \!b\! & \!a+d \\ [-0.5ex] 1\! & \!d\! & \!c\! & \!a+b
\end{vmatrix}$](img2236.png)
(6)![$ \begin{vmatrix}
a\! & \!-a\! & \!-a\! & \!-a \\ [-0.5ex] b\! & \!b\! & \!-b\! ...
...x] c\! &
c\! & \!c\! & \!-c \\ [-0.5ex] d\! & \!d\! & \!d\! & \!d
\end{vmatrix}$](img2237.png) (7)
(7)
![$ \begin{vmatrix}
a+b+c\! & \!-c\! & \!-b \\ [-0.5ex] -c\! & \!a+b+c\! & \!-a \\ [-0.5ex] -b\! &
-a\! & \!a+b+c
\end{vmatrix}$](img2238.png) (8)
(8)
![$ \begin{vmatrix}
1\! & \!1\! & \!1\! & \!1 \\ [-0.5ex] 1\! & \!1+x\! & \!1\! & ...
...1\! &
1\! & \!1+y\! & \!1 \\ [-0.5ex] 1\! & \!1\! & \!1\! & \!1+z
\end{vmatrix}$](img2239.png)
(9)![$ \begin{vmatrix}
x+1\! & \!y\! & \!z\! & \!w \\ [-0.5ex] x\! & \!y+1\! & \!z\! ...
...x\! &
y\! & \!z+1\! & \!w \\ [-0.5ex] x\! & \!y\! & \!z\! & \!w+1
\end{vmatrix}$](img2240.png) (10)
(10)
![$ \begin{vmatrix}
x-2\! & \!4\! & \!3 \\ [-0.5ex] 1\! & \!x+1\! & \!-2 \\ [-0.5ex] 0\! &
0\! & \!x-4
\end{vmatrix}$](img2241.png) (11)
(11)
![$ \begin{vmatrix}
x-1\! & \!3\! & \!-3 \\ [-0.5ex] -3\! & \!x+5\! & \!-3 \\ [-0.5ex] -6\! &
6\! & \!x-4
\end{vmatrix}$](img2242.png)
(12)![$ \begin{vmatrix}
1\! & \!a^2-bc\! & \!a^4 \\ [-0.5ex] 1\! & \!b^2-ca\! & \!b^4 \\ [-0.5ex] 1\! &
c^2-ab\! & \!c^4
\end{vmatrix}$](img2243.png) (13)
(13)
![$ \begin{vmatrix}
a\! & \!abc\! & \!a^2 \\ [-0.5ex] b\! & \!abc\! & \!b^2 \\ [-0.5ex] c\! &
abc\! & \!c^2
\end{vmatrix}$](img2244.png) (14)
(14)
![$ \begin{vmatrix}
b^2+c^2\! & \!ab\! & \!ac \\ [-0.5ex] ab\! & \!c^2+a^2\! & \!bc \\ [-0.5ex] ca\! &
bc\! & \!a^2+b^2
\end{vmatrix}$](img2245.png)
(1)
![$ \begin{vmatrix}
1\! & \!1\! & \!1 \\ [-0.5ex] a\! & \!b\! & \!c \\ [-0.5ex] a^2\! &
b^2\! & \!c^2
\end{vmatrix}$](img2232.png) (2)
(2)
![$ \begin{vmatrix}
a\! & \!b\! & \!c \\ [-0.5ex] a^2\! & \!b^2\! & \!c^2 \\ [-0.5ex] b+c\! &
c+a\! & \!a+b
\end{vmatrix}$](img2233.png) (3)
(3)
![$ \begin{vmatrix}
a\! & \!b\! & \!b\! & \!b \\ [-0.5ex] a\! & \!b\! & \!a\! & \!...
...ex] a\! &
a\! & \!b\! & \!a \\ [-0.5ex] b\! & \!b\! & \!b\! & \!a
\end{vmatrix}$](img2234.png) (4)
(4)
![$ \begin{vmatrix}
0\! & \!a\! & \!b\! & \!c \\ [-0.5ex] a\! & \!0\! & \!c\! & \!...
...ex] b\! &
c\! & \!0\! & \!a \\ [-0.5ex] c\! & \!b\! & \!a\! & \!0
\end{vmatrix}$](img2235.png) (5)
(5)
![$ \begin{vmatrix}
1\! & \!a\! & \!d\! & \!b+c \\ [-0.5ex] 1\! & \!b\! & \!a\! & ...
...1\! &
c\! & \!b\! & \!a+d \\ [-0.5ex] 1\! & \!d\! & \!c\! & \!a+b
\end{vmatrix}$](img2236.png)
(6)
![$ \begin{vmatrix}
a\! & \!-a\! & \!-a\! & \!-a \\ [-0.5ex] b\! & \!b\! & \!-b\! ...
...x] c\! &
c\! & \!c\! & \!-c \\ [-0.5ex] d\! & \!d\! & \!d\! & \!d
\end{vmatrix}$](img2237.png) (7)
(7)
![$ \begin{vmatrix}
a+b+c\! & \!-c\! & \!-b \\ [-0.5ex] -c\! & \!a+b+c\! & \!-a \\ [-0.5ex] -b\! &
-a\! & \!a+b+c
\end{vmatrix}$](img2238.png) (8)
(8)
![$ \begin{vmatrix}
1\! & \!1\! & \!1\! & \!1 \\ [-0.5ex] 1\! & \!1+x\! & \!1\! & ...
...1\! &
1\! & \!1+y\! & \!1 \\ [-0.5ex] 1\! & \!1\! & \!1\! & \!1+z
\end{vmatrix}$](img2239.png)
(9)
![$ \begin{vmatrix}
x+1\! & \!y\! & \!z\! & \!w \\ [-0.5ex] x\! & \!y+1\! & \!z\! ...
...x\! &
y\! & \!z+1\! & \!w \\ [-0.5ex] x\! & \!y\! & \!z\! & \!w+1
\end{vmatrix}$](img2240.png) (10)
(10)
![$ \begin{vmatrix}
x-2\! & \!4\! & \!3 \\ [-0.5ex] 1\! & \!x+1\! & \!-2 \\ [-0.5ex] 0\! &
0\! & \!x-4
\end{vmatrix}$](img2241.png) (11)
(11)
![$ \begin{vmatrix}
x-1\! & \!3\! & \!-3 \\ [-0.5ex] -3\! & \!x+5\! & \!-3 \\ [-0.5ex] -6\! &
6\! & \!x-4
\end{vmatrix}$](img2242.png)
(12)
![$ \begin{vmatrix}
1\! & \!a^2-bc\! & \!a^4 \\ [-0.5ex] 1\! & \!b^2-ca\! & \!b^4 \\ [-0.5ex] 1\! &
c^2-ab\! & \!c^4
\end{vmatrix}$](img2243.png) (13)
(13)
![$ \begin{vmatrix}
a\! & \!abc\! & \!a^2 \\ [-0.5ex] b\! & \!abc\! & \!b^2 \\ [-0.5ex] c\! &
abc\! & \!c^2
\end{vmatrix}$](img2244.png) (14)
(14)
![$ \begin{vmatrix}
b^2+c^2\! & \!ab\! & \!ac \\ [-0.5ex] ab\! & \!c^2+a^2\! & \!bc \\ [-0.5ex] ca\! &
bc\! & \!a^2+b^2
\end{vmatrix}$](img2245.png)
問 4.85 (行列式の性質)
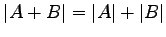 は一般的には成り立たない.その例をあげよ.
は一般的には成り立たない.その例をあげよ.
問 4.86 (行列式の性質)
 が正則行列ならば,
が正則行列ならば,
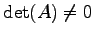 であり,
であり,
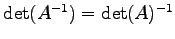 であることを示せ.
であることを示せ.
問 4.87 (行列式の性質)
 ,
,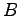 ,
,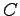 が
が 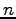 次正方行列のとき,
次正方行列のとき,
![$ \begin{vmatrix}
A\! & \!B \\ [-0.5ex] C\! & \!O
\end{vmatrix}$](img2249.png) を求めよ.
を求めよ.
![$ \begin{vmatrix}
A\! & \!B \\ [-0.5ex] C\! & \!O
\end{vmatrix}$](img2249.png) を求めよ.
を求めよ.
問 4.88 (行列式の性質)
 ,
,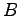 が
が 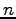 次正方行列のとき,
次正方行列のとき,
![$ \begin{vmatrix}
A\! & \!B \\ [-0.5ex] B\! & \!A
\end{vmatrix}=
\begin{vmatrix}
A+B
\end{vmatrix}\begin{vmatrix}
A-B
\end{vmatrix}$](img2250.png) を示せ.
を示せ.
![$ \begin{vmatrix}
A\! & \!B \\ [-0.5ex] B\! & \!A
\end{vmatrix}=
\begin{vmatrix}
A+B
\end{vmatrix}\begin{vmatrix}
A-B
\end{vmatrix}$](img2250.png) を示せ.
を示せ.
平成20年2月2日