4.14 余因子行列
定義 4.89 (余因子行列)
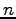 次正方行列
次正方行列  に対して
に対して
と定義される行列を の余因子行列と呼ぶ.
の余因子行列と呼ぶ.
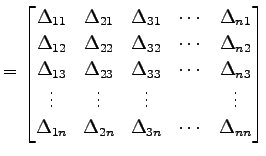 |
(759) |
と定義される行列を
注意 4.90 (余因子行列)
余因子行列
![$ \widetilde{A}=[\Delta_{ji}]$](img2253.png) の
成分の添字は転置行列のならび方であることに注意する.
の
成分の添字は転置行列のならび方であることに注意する.
定理 4.91 (余因子行列の性質)
正方行列  とその余因子行列
とその余因子行列 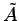 に対して
に対して
が成立する.
である. これは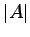 の第
の第 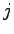 行の余因子展開だから
行の余因子展開だから
となる. 第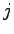 行目に第
行目に第 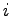 行目の成分がならぶ.
行目の成分がならぶ.
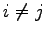 であるとき第
であるとき第 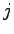 行目と第
行目と第 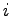 行目は同じ行となるから,
行列式は 0 となる.
行目は同じ行となるから,
行列式は 0 となる.
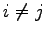 のときは,行列式は
のときは,行列式は 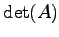 と等しい.
よって,
と等しい.
よって,
を得る.以上より
が示される.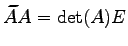 も
同様に示される.
も
同様に示される.
| (760) |
が成立する.
(証明)
![]() ,
,
![]() ,
,
![]() とおく.
積の定義より
とおく.
積の定義より
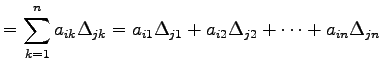 |
(761) |
である. これは
 |
(762) |
となる. 第
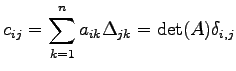 |
(763) |
を得る.以上より
| (764) |
が示される.
平成20年2月2日