4.15 余因子行列と逆行列
定理 4.92 (行列式と行列の正則性)
正方行列  に対して,
に対して,
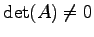 のとき
のとき  は正則である.
は正則である.
であるから,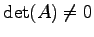 とすると各辺を
とすると各辺を 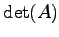 で割って
で割って
が成り立つ.よって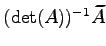 は
は
 の逆行列であり,
の逆行列であり, は正則である.
は正則である.
(証明)
定理
| (765) |
であるから,
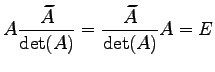 |
(766) |
が成り立つ.よって
定理 4.93 (余因子行列と逆行列)
正方行列  に対して,
に対して,
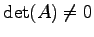 のとき
のとき  の逆行列は
の逆行列は
で与えられる.
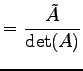 |
(767) |
で与えられる.
定理 4.94 (逆行列が存在するための十分条件)
正方行列  ,
, 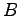 に対して
に対して 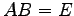 (または
(または 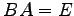 )が成立するとき,
)が成立するとき,
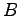 は
は  の逆行列となる.
の逆行列となる.
が成り立つ. これより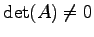 を得る.
よって,
を得る.
よって,
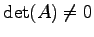 のとき
のとき  は正則であるから,
逆行列
は正則であるから,
逆行列 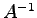 をもつ.
さらに
をもつ.
さらに 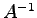 が存在することを用いると
が存在することを用いると
が成り立つ.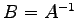 が示された.
が示された.
(証明)
![]() より,両辺の行列式をとると
より,両辺の行列式をとると
| (768) |
が成り立つ. これより
| (769) |
が成り立つ.
例 4.95 (余因子行列による逆行列の計算の具体例)
 のとき逆行列は
のとき逆行列は
である. のとき逆行列は
のとき逆行列は
である.
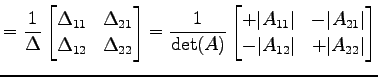 |
(770) | |
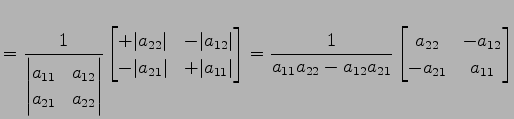 |
(771) |
である.
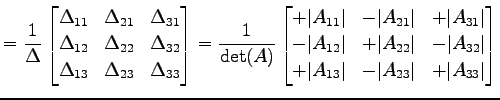 |
(772) | |
![$\displaystyle = \frac{1}{ \begin{vmatrix}a_{11} & a_{12} & a_{13} \\ a_{21} & a...
...in{vmatrix}a_{11} & a_{12} \\ a_{21} & a_{22} \end{vmatrix} \end{array} \right]$](img2273.png) |
(773) |
である.
例 4.96 (余因子行列による逆行列の計算例)
行列
の逆行列を求める. 行列式は
であるから, 逆行列は
で与えられる.
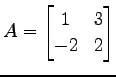 |
(774) |
の逆行列を求める. 行列式は
| (775) |
であるから, 逆行列は
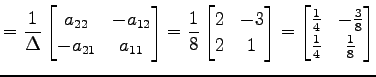 |
(776) |
で与えられる.
例 4.97 (余因子行列による逆行列の計算例)
行列
の逆行列を求める. 小行列の行列式は
であり,行列式は
であるので, 逆行列は
と与えられる.
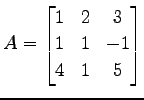 |
(777) |
の逆行列を求める. 小行列の行列式は
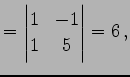 |
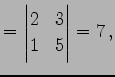 |
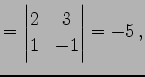 |
(778) | |||
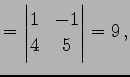 |
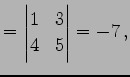 |
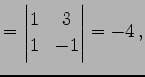 |
(779) | |||
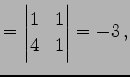 |
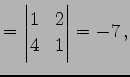 |
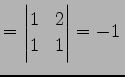 |
(780) |
であり,行列式は
 |
(781) |
であるので, 逆行列は
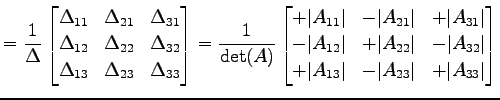 |
(782) | |
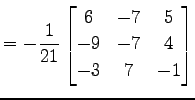 |
(783) |
と与えられる.
平成20年2月2日