5.1 線形変換で向きが変わらないベクトル
線形変換
![]()
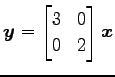 を
考える.
を
考える.
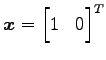 のとき
のとき
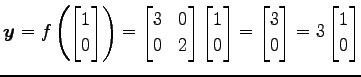 |
となり,元のベクトルから向きを変えず
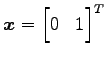 のときでは
のときでは
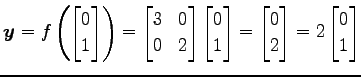 |
となり,元のベクトルから向きを変えず
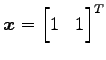 のときでは
のときでは
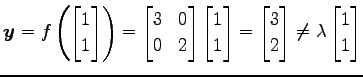 |
となり,元のベクトルと向きが変わる.
同様に他の線形変換
![]()
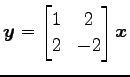 の
場合を考える.
このとき
の
場合を考える.
このとき
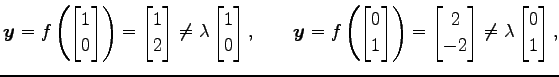 |
||
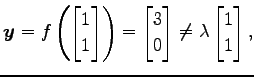 |
||
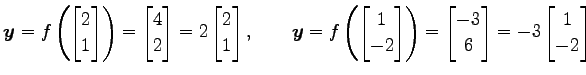 |
となる. ベクトル
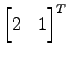 は
向きを変えず元のベクトルの
は
向きを変えず元のベクトルの 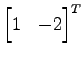 は
向きを変えず元のベクトルの
は
向きを変えず元のベクトルの 線形変換には向きを変えないベクトルが存在する. そのベクトルは線形変換それぞれに対して固有に定まる. このベクトルのことを固有ベクトルという. また,定数倍の定数のことを固有値という.
平成20年2月2日