5.2 固有値と固有ベクトル
定義 5.1 (固有値問題)
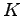 (
(
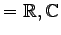 ) 上の
ベクトル空間
) 上の
ベクトル空間  における線形変換
における線形変換 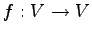 が方程式
が方程式
をみたすとする. このとき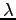 を
を  の固有値(eigenvalue)といい,
の固有値(eigenvalue)といい,
 を固有値
を固有値 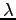 に属する
に属する  の
固有ベクトル(eigenvector)という.
また,方程式(☆)を固有方程式(eigen-equation)といい,
この方程式の固有値と固有ベクトルを求める問題を
固有値問題(eigen-problem)という.
の
固有ベクトル(eigenvector)という.
また,方程式(☆)を固有方程式(eigen-equation)といい,
この方程式の固有値と固有ベクトルを求める問題を
固有値問題(eigen-problem)という.
をみたすとする. このとき
注意 5.2 (固有値問題)
線形変換  は必ず
は必ず
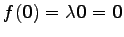 をみたすので,
零ベクトル
をみたすので,
零ベクトル 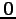 は線形変換
は線形変換  によって
自分自身のスカラー
によって
自分自身のスカラー 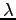 倍に写される.
このとき
倍に写される.
このとき 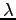 は任意である.
よって
は任意である.
よって 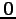 は固有ベクトルと定義しない.
は固有ベクトルと定義しない.
例 5.3 (単振動系の固有振動の問題)
重さ 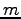 の剛体がバネ定数
の剛体がバネ定数 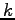 のバネにつながれ
動摩擦係数
のバネにつながれ
動摩擦係数 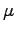 の床におかれている.
バネの伸びを
の床におかれている.
バネの伸びを 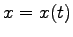 とする.
剛体に外力
とする.
剛体に外力 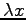 があるとき
運動方程式は
があるとき
運動方程式は
と表される.微分演算子を
とおくと,
と書ける. これは固有方程式である. この固有値問題を力学では 単振動系の固有振動の問題という.
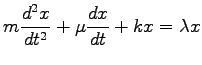 |
と表される.微分演算子を
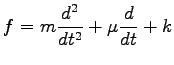 |
とおくと,
と書ける. これは固有方程式である. この固有値問題を力学では 単振動系の固有振動の問題という.
例 5.4 (固有値,固有ベクトルの具体例)
線形変換
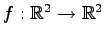 ;
;
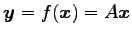 を考える.
ただし,
を考える.
ただし,
とする. このとき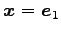 ,
,
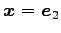 を代入すると
を代入すると
が成り立つ. よって線形変換 の固有値は
の固有値は 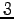 と
と 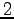 である.
固有値
である.
固有値 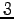 に属する
に属する  の固有ベクトルは
の固有ベクトルは 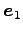 であり,
固有値
であり,
固有値 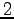 に属する
に属する  の固有ベクトルは
の固有ベクトルは 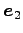 である.
である.
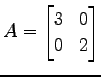 |
とする. このとき
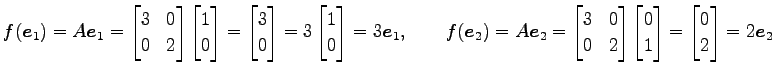 |
が成り立つ. よって線形変換
例 5.5 (固有値,固有ベクトルの具体例)
線形変換
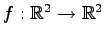 ;
;
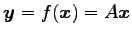 を考える.
ただし,
を考える.
ただし,
とする. このとき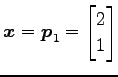 を
代入すると
を
代入すると
が成り立つ. よって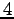 は線形変換
は線形変換  の固有値である.
の固有値である.
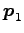 は固有値
は固有値 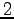 に属する
に属する  の固有ベクトルである.
次に
の固有ベクトルである.
次に
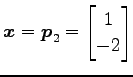 を
代入すると
を
代入すると
が成り立つ. よって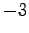 は線形変換
は線形変換  の固有値である.
の固有値である.
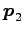 は固有値
は固有値 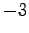 に属する
に属する  の固有ベクトルである.
の固有ベクトルである.
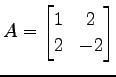 |
とする. このとき
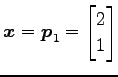 を
代入すると
を
代入すると
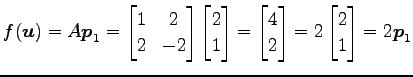 |
が成り立つ. よって
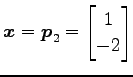 を
代入すると
を
代入すると
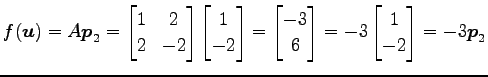 |
が成り立つ. よって
平成20年2月2日