1.9 恒等写像,逆写像
定義 1.33 (恒等写像)
写像  がすべての
がすべての 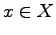 に対して
に対して
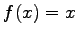 をみたすとき,
をみたすとき,
 を恒等写像(identity mapping)といい,
を恒等写像(identity mapping)といい,
と表記する.
と表記する.
例 1.34 (恒等写像の具体例)
写像
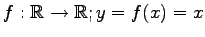 は
恒等写像である.
は
恒等写像である.
定義 1.35 (逆写像)
写像 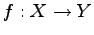 ,
, 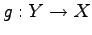 の合成写像が
の合成写像が
をみたすとき,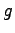 を
を  の逆写像(inverse mapping)といい,
の逆写像(inverse mapping)といい,
と表記する.
をみたすとき,
と表記する.
例 1.36 (逆写像の具体例)
写像
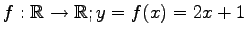 の
逆写像は
の
逆写像は
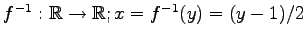 である.
である.
例 1.37 (逆写像をもたない具体例)
写像
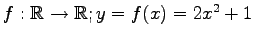 の
逆写像
の
逆写像 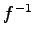 は存在しない.
は存在しない.
平成20年2月2日