5.22 正規行列
定義 5.58 (共役行列)
行列
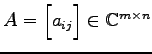 に対して
に対して
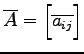 と定義する.
と定義する.
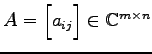 に対して
に対して
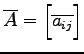 と定義する.
と定義する.
定義 5.59 (共役転置行列)
行列
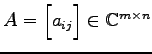 に対して
共役転置行列を
に対して
共役転置行列を
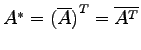 と定義する.
と定義する.
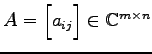 に対して
共役転置行列を
に対して
共役転置行列を
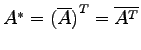 と定義する.
と定義する.
定義 5.60 (正規行列)
正方行列  が
が
をみたすとき を正規行列(normal matrix)という.
を正規行列(normal matrix)という.
をみたすとき
例 5.61 (正規行列)
正規行列には次のものがある:
- 対称行列
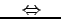
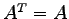
- 歪対称行列
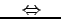
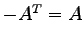
- エルミート行列
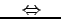
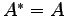
- 歪エルミート行列
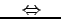
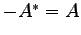
- 直交行列
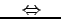
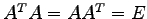
- ユニタリー行列
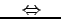
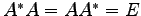
定理 5.62 (正規行列の固有値)
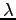 ,
, 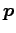 が正規行列
が正規行列  の
固有値とその固有ベクトルであるとき,
の
固有値とその固有ベクトルであるとき,
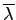 ,
, 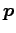 は
は 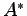 の固有値と
その固有ベクトルとなる.
の固有値と
その固有ベクトルとなる.
より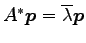 を得る.
を得る.
(証明)
より
定理 5.63 (正規行列の固有ベクトル)
正規行列の相異なる固有ベクトルは直交する.
が成り立つ.よって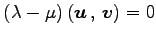 であり,
であり,
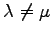 であるから,
であるから,
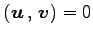 を得る.
を得る.
(証明)
固有値 ![]() ,
, ![]() (
(
![]() ) の固有ベクトルを
) の固有ベクトルを
![]() ,
, ![]() とする.
このとき
とする.
このとき
![]() ,
,
![]() である.
これと
である.
これと
![]() より
より
が成り立つ.よって
平成20年2月2日