5.25 3 慼覆憊墊昫及覆剩祭
拺 5.74 (覆憊墊昫及覆剩祭及填蟲拺)
覆憊墊昫
毛躂跟墊昫匹覆剩祭允月‘ 及裔肣聶嫩摯反
及裔肣聶嫩摯反
匹丐月井日﹞ 裔肣襖反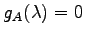 方曰
方曰
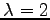 (2 褐),
(2 褐),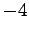 午卅月‘
午卅月‘
方曰﹞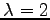 午
午
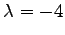 卞
簞允月裔肣矛弁玄伙反公木冗木
卞
簞允月裔肣矛弁玄伙反公木冗木
午卅月‘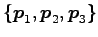 反1 慼つ峏匹丐月井日﹞
反1 慼つ峏匹丐月井日﹞
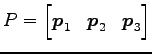 反懇禮午卅月‘
仄井仄
反懇禮午卅月‘
仄井仄 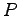 反躂跟墊昫匹反卅中及匹﹞
躂跟墊昫午卅月方丹卞裔肣矛弁玄伙毛薊太躂允‘
反躂跟墊昫匹反卅中及匹﹞
躂跟墊昫午卅月方丹卞裔肣矛弁玄伙毛薊太躂允‘
匹丐月井日﹞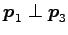 ,
,
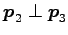 午卅月‘
午卅月‘
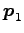 ,
, 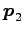 毛弘仿丞’扑亙立永玄及躂跟祭芊匹
懇筋躂跟祭仄﹞
毛弘仿丞’扑亙立永玄及躂跟祭芊匹
懇筋躂跟祭仄﹞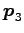 反懇筋祭允木壬方中‘
反懇筋祭允木壬方中‘
午云仁午﹞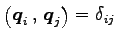 (
(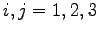 )
互嶽曰峏切懇筋躂跟煙午卅月‘
動曉方曰墊昫
)
互嶽曰峏切懇筋躂跟煙午卅月‘
動曉方曰墊昫  反
反
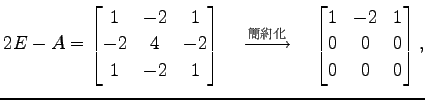
午躂跟墊昫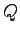 匹覆剩祭今木月‘
匹覆剩祭今木月‘
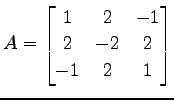 |
毛躂跟墊昫匹覆剩祭允月‘
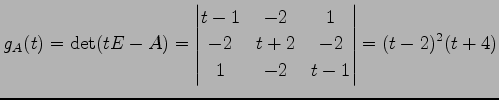 |
匹丐月井日﹞ 裔肣襖反
 |
||
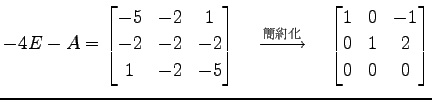 |
方曰﹞
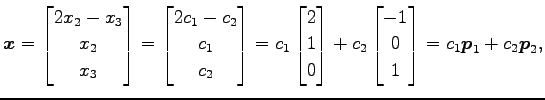 |
||
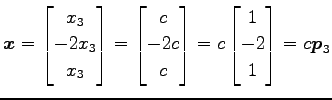 |
午卅月‘
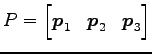 反懇禮午卅月‘
仄井仄
反懇禮午卅月‘
仄井仄 匹丐月井日﹞
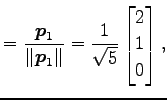 |
||
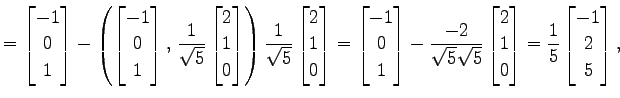 |
||
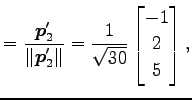 |
||
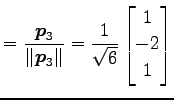 |
午云仁午﹞
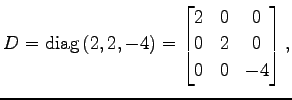 |
||
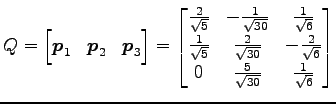 |
午躂跟墊昫
鏜啦 5.75 (覆憊墊昫及裔肣塢棉)
瞬溥庍晶
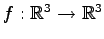 ;
;
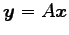 及
裔肣塢棉反
及
裔肣塢棉反
匹丐月‘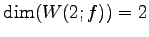 ,
,
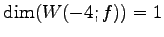 ,
,
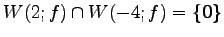 方曰
方曰
毛ぜ月‘ 裔肣塢棉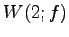 ,
, 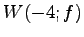 反
反
 及躂狟坌荸匹丐月‘
引凶﹞
唱卅月裔肣襖卞簞允月裔肣矛弁玄伙反躂跟允月及匹﹞
裔肣塢棉手躂跟仄
及躂狟坌荸匹丐月‘
引凶﹞
唱卅月裔肣襖卞簞允月裔肣矛弁玄伙反躂跟允月及匹﹞
裔肣塢棉手躂跟仄
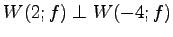 毛ぜ月‘
毛ぜ月‘
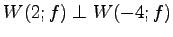 午(↗)方曰﹞
午(↗)方曰﹞
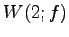 反
反
 卞云仃月
卞云仃月 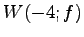 及躂跟怀塢棉午卅月‘
引凶菅卞
及躂跟怀塢棉午卅月‘
引凶菅卞
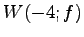 反
反
 卞云仃月
卞云仃月 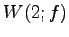 及躂跟怀塢棉午卅月‘
及躂跟怀塢棉午卅月‘
匹丐月‘
毛ぜ月‘ 裔肣塢棉
尪嶽20ヵ2畸2ゥ