6.2 2 次曲線の中心
2 次曲線は
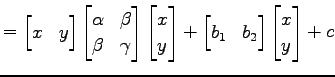 |
||
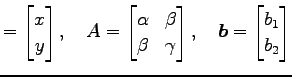 |
と表される.
定義 6.4 (曲線の中心)
曲線 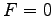 が点
が点 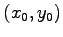 に関して点対称なとき,
に関して点対称なとき,
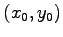 を曲線
を曲線 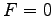 の中心という.
の中心という.
定理 6.5 ( 2 次曲線の中心)
2 次曲線
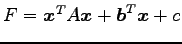 に
中心が存在するための必要十分条件は,
に
中心が存在するための必要十分条件は,
 が正則であることである.
が正則であることである.
に対して,
をみたす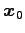 が一意に存在することである.
任意の
が一意に存在することである.
任意の
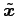 に対して成立するためには
に対して成立するためには
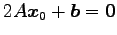 でなければならない.
よって
でなければならない.
よって
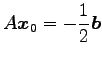 を得る.
この方程式で解
を得る.
この方程式で解 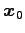 が一意に存在するための
必要十分条件は
が一意に存在するための
必要十分条件は  が正則となることである.
が正則となることである.
(証明)
曲線 ![]() がある点
がある点 ![]() に関して
点対称であるための必要十分条件は,
すべての
に関して
点対称であるための必要十分条件は,
すべての ![]() 上の点
上の点
![]() に対して,
に対して,
![]() も
も ![]() 上の点となるような
上の点となるような
![]() が一意に存在ことである.
すなわち,
が一意に存在ことである.
すなわち,
| 0 | ||
に対して,
をみたす
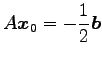 を得る.
この方程式で解
を得る.
この方程式で解
定義 6.6 (有心,無心 2 次曲線)
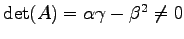 となる 2 次曲線を
有心 2 次曲線という.
となる 2 次曲線を
有心 2 次曲線という.
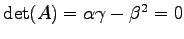 となる 2 次曲線を
無心 2 次曲線という.
となる 2 次曲線を
無心 2 次曲線という.
例 6.7 (有心,無心 2 次曲線)
楕円形と双曲形は有心 2 次曲線である.
放物形は無心 2 次曲線である.
平成20年2月2日