6.4 2 次曲線の標準形
定理 6.9 (2 次曲線の標準形)
原点を中心とする有心 2 次曲線
は回転変換で標準形
に写される.
の係数 は対称行列なので直交行列
は対称行列なので直交行列 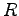 により対角化される.
すなわち,
により対角化される.
すなわち,
が成り立つ. これより,
であることを用いると,
となる. ただし,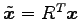 ,
,
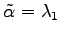 ,
,
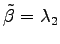 とおく.
とおく.
は回転変換で標準形
に写される.
(証明) 2 次曲線
の係数
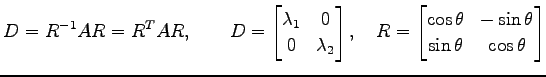 |
が成り立つ. これより,
であることを用いると,
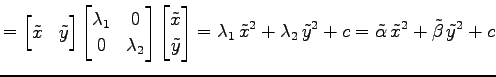 |
となる. ただし,
定理 6.10 ( 2 次曲線の分類)
2 次曲線
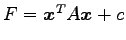 は
は
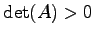 のとき楕円形であり,
のとき楕円形であり,
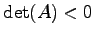 のとき双曲形であり,
のとき双曲形であり,
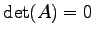 のとき放物形である.
のとき放物形である.
と
より分類される.
(証明)
と
より分類される.
例 6.11 ( 2 次曲線のグラフの具体例)
2 次曲線
のグラフを描く. まず,
より,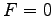 は双曲形である.
次に
は双曲形である.
次に  を直交行列
を直交行列 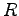 で対角化すると,
で対角化すると,
である.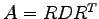 より
より
と標準形を得る. ただし,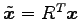 とおく.
よって
とおく.
よって
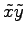 軸の 2 次曲線は双曲線
軸の 2 次曲線は双曲線
となる.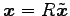 より
より 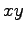 軸では
軸では
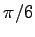 回転したグラフである.
回転したグラフである.
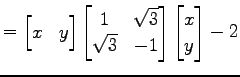 |
||
のグラフを描く. まず,
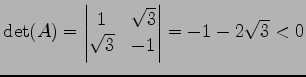 |
より,
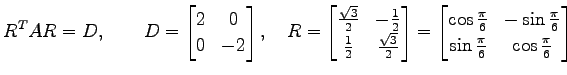 |
である.
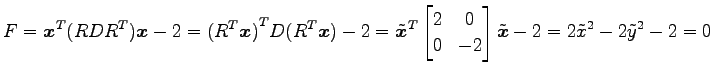 |
と標準形を得る. ただし,
となる.
![\includegraphics[width=0.4\textwidth]{soukyokusen.eps}](img3666.png) |
![\includegraphics[width=0.4\textwidth]{soukyokusen-R.eps}](img3667.png) |
| (a)
|
(b) |
例 6.12 ( 2 次曲線のグラフの具体例)
2 次曲線
のグラフを描く. まず,
より,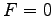 は楕円形である.
有心であるから中心
は楕円形である.
有心であるから中心  を求める.
を求める.
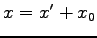 ,
, 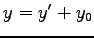 とおき平行移動する.
とおき平行移動する.
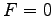 へ代入すると,
へ代入すると,
となる.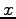 ,
, 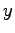 の項が消えるとき,
原点が中心となるので,
の項が消えるとき,
原点が中心となるので,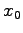 ,
, 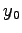 は
連立方程式
は
連立方程式
をみたさなければならない. この方程式は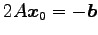 とも書けるので,
中心
とも書けるので,
中心 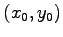 の位置ベクトルは
の位置ベクトルは
と得られる. あらためて
とおき, 座標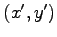 について書き直すと,
について書き直すと,
と表される. 次に行列 の固有値は
の固有値は 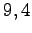 であり,
直交行列
であり,
直交行列 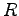 で対角化すると,
で対角化すると,
である. ここで,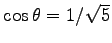 ,
,
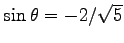 より,
より,
 である.
である.
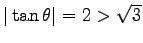 より
より
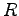 は負の方向に
は負の方向に 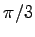 より少し大きく回転させる.
より少し大きく回転させる.
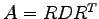 より
より
と標準形が得られる. ここで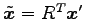 とおいた.
とおいた.
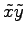 軸平面では 2 次曲線は
軸平面では 2 次曲線は
となる. これは中心が原点の楕円形である. この曲線を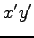 軸平面に戻す.
軸平面に戻す.
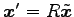 であるから,
時計回りに角
であるから,
時計回りに角 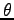 の回転させたグラフを
の回転させたグラフを
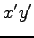 軸平面に描く.
さらに平行移動
軸平面に描く.
さらに平行移動
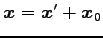 より,
楕円の中心が
より,
楕円の中心が 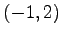 となるように
となるように
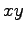 軸平面にグラフを描く.
軸平面にグラフを描く.
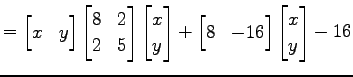 |
|||
のグラフを描く. まず,
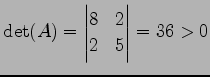 |
より,
となる.
をみたさなければならない. この方程式は
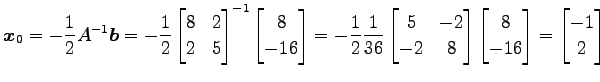 |
と得られる. あらためて
とおき, 座標
と表される. 次に行列
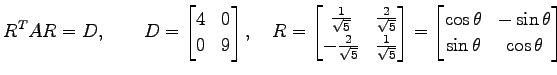 |
である. ここで,
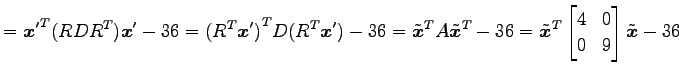 |
||
と標準形が得られる. ここで
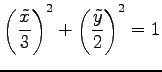 |
となる. これは中心が原点の楕円形である. この曲線を
![\includegraphics[width=0.4\textwidth]{daen.eps}](img3699.png) |
![\includegraphics[width=0.4\textwidth]{daen-R.eps}](img3700.png) |
| (a)
|
(b) |
![\includegraphics[width=0.4\textwidth]{daen-RS.eps}](img3701.png) |
|
| (c) |
例 6.13 (放物形)
2 次曲線
のグラフを書く. まず,
とおく.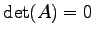 より
より 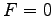 は放物形である.
は放物形である.
 は無心曲線であるから中心はない.
は無心曲線であるから中心はない.
 を対角化すると,
を対角化すると,
となる.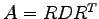 を
を 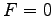 に代入すると
に代入すると
となる. ここで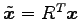 ,
,
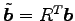 とおいた.
とおいた.
より,2 次曲線は
となる. 書き直すと
となる. これは頂点が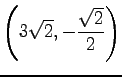 の放物線である.
また,この放物線は
直線
の放物線である.
また,この放物線は
直線
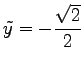 に線対称であり,
直線
に線対称であり,
直線
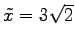 に接している.
に接している.
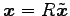 を用いて
を用いて
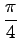 回転すると
回転すると
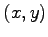 に関する曲線に戻る.
頂点は
に関する曲線に戻る.
頂点は
より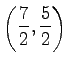 となる.
また,
となる.
また,
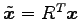 より,
より,
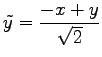 を
を
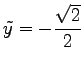 に代入すると,
に代入すると,
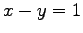 となる.
となる.
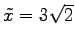 に
に
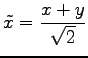 を代入すると,
を代入すると,
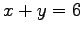 となる.
よって
となる.
よって 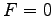 は
頂点が
は
頂点が 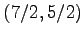 の放物形で,
直線
の放物形で,
直線 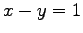 ,
, 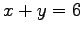 を軸とする放物線である.
を軸とする放物線である.
のグラフを書く. まず,
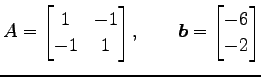 |
とおく.
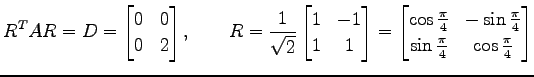 |
となる.
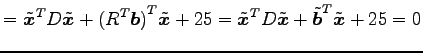 |
となる. ここで
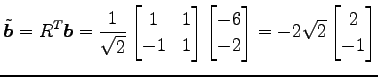 |
より,2 次曲線は
となる. 書き直すと
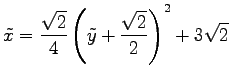 |
となる. これは頂点が
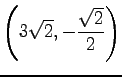 の放物線である.
また,この放物線は
直線
の放物線である.
また,この放物線は
直線
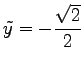 に線対称であり,
直線
に線対称であり,
直線
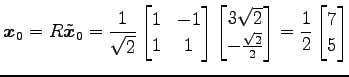 |
より
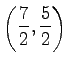 となる.
また,
となる.
また,
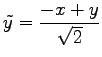 を
を
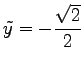 に代入すると,
に代入すると,
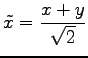 を代入すると,
を代入すると,
平成20年2月2日