2.3 実ベクトルの内積
定義 2.8 (内積)
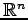 の 2 つのベクトル
の 2 つのベクトル
に対して
なる 2 項演算を内積(inner product)という.
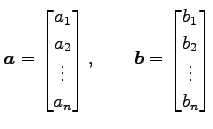 |
に対して
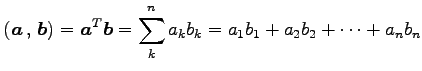 |
なる 2 項演算を内積(inner product)という.
例 2.9 (内積の具体例)
ベクトル
の内積は
である. ベクトル
の内積は
である.
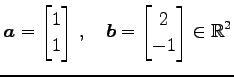 |
の内積は
である. ベクトル
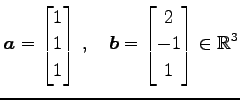 |
の内積は
である.
定理 2.10 (内積の性質)
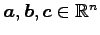 と
と
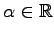 に対して
に対して
- (i).
- (内積の交換則)
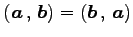 .
.
- (ii).
- (内積の分配則)
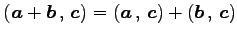 .
.
- (iii).
- (内積のスカラー倍の結合則)
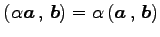 ,
,
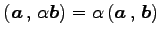 .
.
- (iv).
-
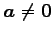 のとき
のとき
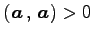
問 2.11 (内積の性質)
これを示せ.
平成20年2月2日