2.5 内積と行列の積
注意 2.17 (行列の積と内積)
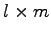 型行列
型行列  を行ベクトルに分割し,
を行ベクトルに分割し,
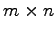 型行列
型行列 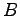 を列ベクトルに分割し
を列ベクトルに分割し
とおく. ただし,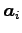 ,
, 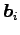 は
は 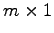 型の列ベクトルである.
このとき積は
型の列ベクトルである.
このとき積は
と表される.
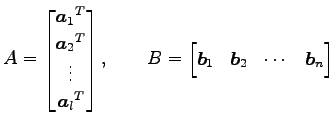 |
とおく. ただし,
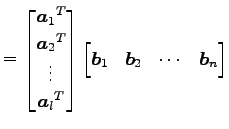 |
||
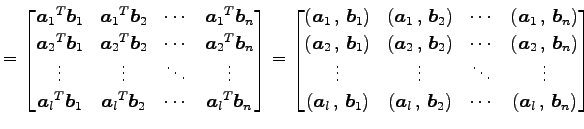 |
と表される.
定理 2.18 (内積の性質)
複素行列
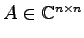 ;
;
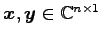 に対して
に対して
が成り立つ. 特に が実行列
が実行列
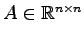 であれば
であれば
が成り立つ.
が成り立つ. 特に
が成り立つ.
(証明)
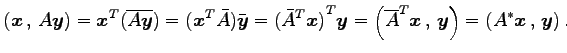 |
平成20年2月2日