2.6 ノルム
定義 2.19 (ノルム)
ベクトル
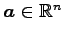 または
または
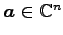 に対して
に対して
をベクトルのノルム(norm)または 長さ(length)という.
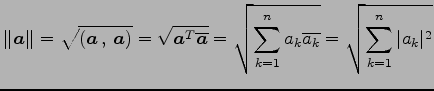 |
をベクトルのノルム(norm)または 長さ(length)という.
注意 2.20 (ノルムの性質)
-
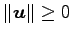 .
.
-
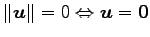 .
.
-
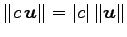 .
.
例 2.21 (ノルムの具体例)
ベトクル
のノルムはそれぞれ
である.
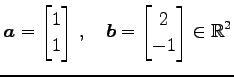 |
のノルムはそれぞれ
である.
例 2.22 (ノルムの具体例)
ベトクル
のノルムはそれぞれ
である.
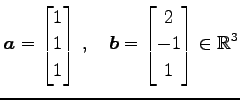 |
のノルムはそれぞれ
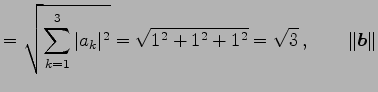 |
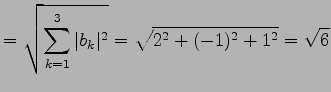 |
である.
例 2.23 (ノルムの具体例)
ベトクル
のノルムは
である.
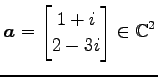 |
のノルムは
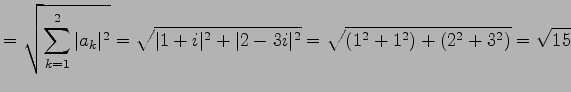 |
である.
例 2.24 (ノルムの具体例)
ベトクル
のノルムは
である.
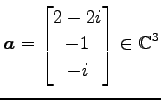 |
のノルムは
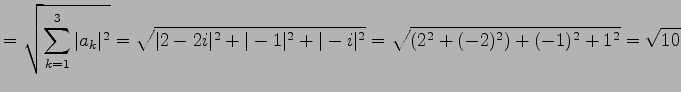 |
である.
平成20年2月2日