2.8 単位ベクトル
定義 2.28 (単位ベクトル)
ノルムが 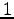 のベクトルを
単位ベクトル(unit vectar)または
正規化されたベクトル(normalized vector) という.
のベクトルを
単位ベクトル(unit vectar)または
正規化されたベクトル(normalized vector) という.
例 2.29 (単位ベクトルの具体例)
ベトクル
は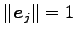 であり全て単位ベクトルである.
であり全て単位ベクトルである.
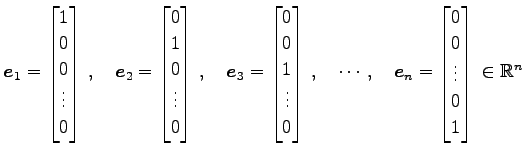 |
は
定義 2.30 (正規化)
あるベクトルを向きが同じで長さが 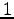 のベクトルに
変換することを正規化(normalization)という.
のベクトルに
変換することを正規化(normalization)という.
例 2.31 (正規化の具体例)
ベクトル
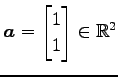 を正規化し,
を正規化し,
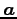 と向きが同じ単位ベクトルを
と向きが同じ単位ベクトルを
と得る.
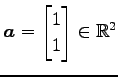 を正規化し,
を正規化し,
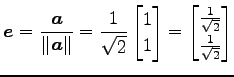 |
と得る.
例 2.32 (正規化の具体例)
ベクトル
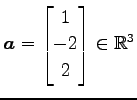 を正規化し,
を正規化し,
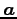 と向きが同じ単位ベクトルを
と向きが同じ単位ベクトルを
と得る.
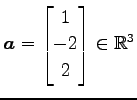 を正規化し,
を正規化し,
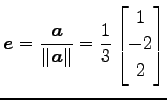 |
と得る.
平成20年2月2日