2.9 ベクトルのなす角
定義 2.33 (ベクトルの成す角)
2 つのベトクル
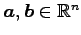 に対して
に対して
により与えられる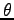 を
ベクトル
を
ベクトル 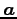 と
と 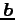 との成す角(angular)という.
また,
との成す角(angular)という.
また,
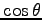 を方向余弦(direction cosine)という.
を方向余弦(direction cosine)という.
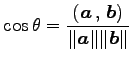 |
により与えられる
注意 2.34 (内積とノルムの比)
シュバルツの不等式より
となることに注意する.
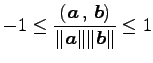 |
となることに注意する.
例 2.35 (成す角の具体例)
ベトクル
を考える.このとき方向余弦は
となるので, 成す角は
である.
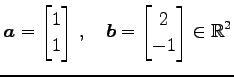 |
を考える.このとき方向余弦は
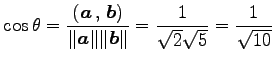 |
となるので, 成す角は
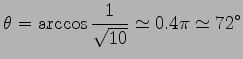 |
である.
例 2.36 (成す角の具体例)
ベトクル
を考える.このとき方向余弦は
となるので, 成す角は
である.
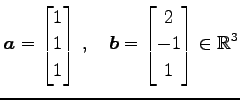 |
を考える.このとき方向余弦は
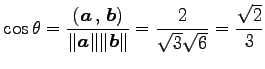 |
となるので, 成す角は
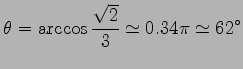 |
である.
平成20年2月2日