2.12 正規直交系
定義 2.46 (正規直交系)
ベクトルの組
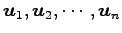 は直交系であり,
かつ,すべてのベクトルが単位ベクトルであるとする.
すなわち,
は直交系であり,
かつ,すべてのベクトルが単位ベクトルであるとする.
すなわち,
をみたすとき, このベクトルの組を正規直交系(orthonormal system)という.
をみたすとき, このベクトルの組を正規直交系(orthonormal system)という.
例 2.47 (基本ベクトルの正規直交性)
基本ベクトル
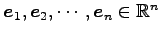 は
正規直交系である.
は
正規直交系である.
問 2.48 (正規直交系の具体例)
次のベクトルの組は正規直交系であることを示せ.
(1)
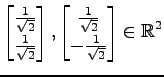 (2)
(2)
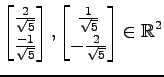 (3)
(3)
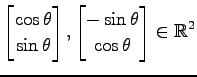
(4)
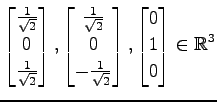 (5)
(5)
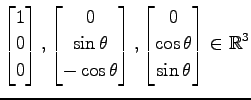
平成20年2月2日